Aufgabe:
Untersuchen Sie, ob jeweils zwei der zu den Graphen gehörenden Funktionen eine Stammfunktion derselben Funktion f sein können. Begründen Sie ihre Antwort.
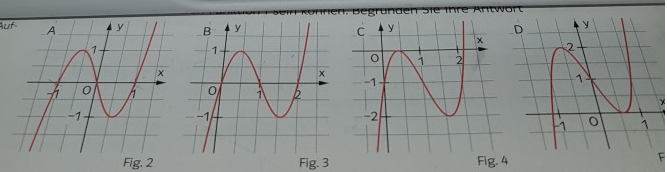
Problem/Ansatz:
Ich verstehe die Aufgabe gar nicht, kann mir jemand bitte die Lösungen ausführlich nennen?