Hallo Alexa,
die allgemeine trigonometrische Form einer komplexen Zahl \(z\) lautet: $$z = |z| \cdot (\cos \arg(z) + i \cdot \arg(z))$$ mit \(\arg(z) = \varphi\). Du schreibst:
Wenn ich die trigonometrische bestimme, dann komme ich erstmal auf \(-\pi/4\) und dann muss ich doch \(\pi/4\) dazu addieren, weil wir uns ja im 2. Quadranten befinden, oder?
Ich weiß nicht, wie Du auf \(-\pi/4\) kommst und addieren musst Du normal auch nichts ... es gilt doch: $$\sin \varphi = \frac{\Im(z)}{|z|} \\ \cos \varphi = \frac{\Re(z)}{|z|}$$ das sieht man am besten in der Gauß'schen Zahlenebene:
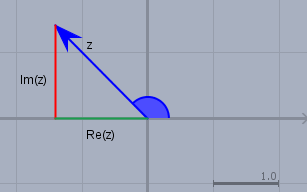
Der blaue Vektor entspricht der Zahl \(z\). Der Imaginärteil ist rot und der Realteil grün markiert. Der Vektor, der Imaginär- und Realteil bilden ein rechtwinkliges Dreieck mit den üblichen trigonometrischen Beziehungen. Der blaue Winkel ist \(\varphi\). Man muss noch bei den Vorzeichen aufpassen. Sinus und Cosinus lassen sich nun berechnen (s.o.): $$\sin \varphi = \frac{\Im(z)}{|z|} = \frac{\sqrt{2}}{2} \\ \cos \varphi = \frac{\Re(z)}{|z|} = \frac{-\sqrt{2}}{2}$$ aus beiden Informationen zusammen(!) folgt nun: $$\varphi = \frac 34 \pi = 135°$$ Nur \(\varphi = 135°\) erfüllt beide Gleichungen. D.h. die Darstellung ist $$z = 2 \cdot \left(\cos \frac{3 \pi}{4} + i \cdot \sin \frac{3 \pi}{4} \right) \\ z = 2 \cdot e^{\frac{3 \pi}{4}}$$
Nachtrag zur Berechnung des Winkels \(\varphi\):
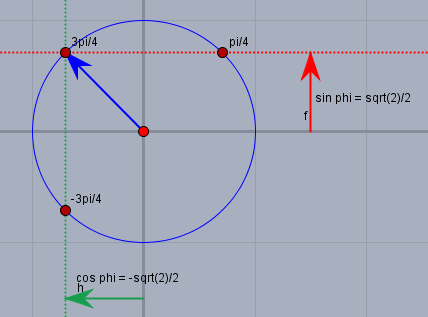
in der Skizze siehst Du die rote gepunktete Linie. Hier ist \(\sin \varphi = \sqrt{2}/2\). Zwei Winkel erfüllen diese Bedingung: zum einen \(\pi/4\) und \(3\pi/4\). Die grüne gepunktete Linie zeigt an, wo \(\cos \varphi = -\sqrt{2}/2\) ist. Das ist bei \(3\pi/4\) und bei \(-3\pi/4\) der Fall. Nur bei \(3\pi/4\) ist sowohl \(\sin \varphi = \sqrt{2}/2\) als auch \(\cos \varphi = -\sqrt{2}/2\) erfüllt. Der Taschenrechner liefert Dir nur Ergebnisse im Intervall \([-\pi/2; +\pi/2]\). Deshalb ist es immer wichtig sich (am besten graphisch) zu veranschaulichen, wo der Winkel wirklich liegt.
Und in diesem Fall brauchst Du doch gar keinen Taschenrechner! Wofür denn?
Gruß Werner