man kann eine Matrix nur invertieren, wenn alle Spalten oder Zeilen linear unabhängig sind.
Berechne also die 3x3-Determinante, die, um die lineare Unabhängigkeit aller Spalten zu gewähen, ungleich null sein muss:$$\begin{vmatrix} 0 & t & 2 \\ t & 0 & 0 \\ 0 & 2t & t^2 \end{vmatrix}\neq 0$$ Du kannst nun mit Hilfe des LaPlaschen Entwicklungssatz die Determinante um eine Dimension reduzieren oder die Regel von Sarrus anwenden.
Laplacescher Entwicklungssatz:
Entwickle nach der 2 Zeile, da diese viele Nullen enthält:$$\begin{vmatrix} 0 & t & 2 \\ t & 0 & 0 \\ 0 & 2t & t^2 \end{vmatrix}=-t\cdot \begin{vmatrix}t&2\\2t & t^2\end{vmatrix}$$ Nun einfach die beiden Hauptdiagonalen miteinander multiplizieren, voneinander abziehen und den Term ungleich null setzen:$$-t\cdot (t\cdot t^2-2\cdot 2t)\neq 0$$$$-t^2(t^2-4)\neq 0$$ Daraus folgt \(t_1=0\) \(\vee\) \(t_2=2\) \(\vee\) \(t_3=-2\)
Das sind diejenigen Werte, für die die Determinante 0 wird, deshalb ist unsere Lösungemenge \(\{t\in \mathbb{R}\backslash\{0,\pm2\}\}\)
Regel von Sarrus:
Hier ist erstmal ein gutes Bild, um zu veranschaulichen, was ich Dir erklären möchte:
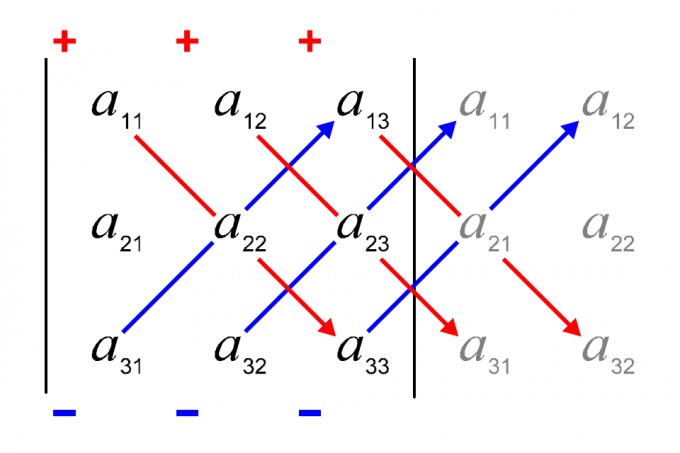
(1) Du trägst die beiden ersten Spalten (von links) neben die Determinante ab
(2) Du multiplizierst alle Werte, die von den einzelen roten Diagonalen verbunden werden und addierst jeweils deren Produkte zusammen.
(3) Du addierst alle Werte, die von den blauen Diagonalen verbunden werden und addierst jeweils deren Produkte zusammen.
(4) Ziehe die Summe von (2) mit (3) ab. Also (2) ist der Minuend und (3) der Subtrahend.