Hallo Daniel,
Da die Winkel in dieser Figur alle rechte Winkel oder 'halbe' rechte Winkel (45°) sind, oder eben nicht von Interesse sind, nützt Sinus- oder Kosinussatz hier auch nichts.
Auf der Hand läge ein schlichte Schnittpunktsberechnung zwischen Gerade und Kreis. Der Kreis ist einfach$$x^2 + y^2 =\left( \frac D2 \right) ^2$$ Und die Gerade sei die Verlängerung des rechten Schenkels.
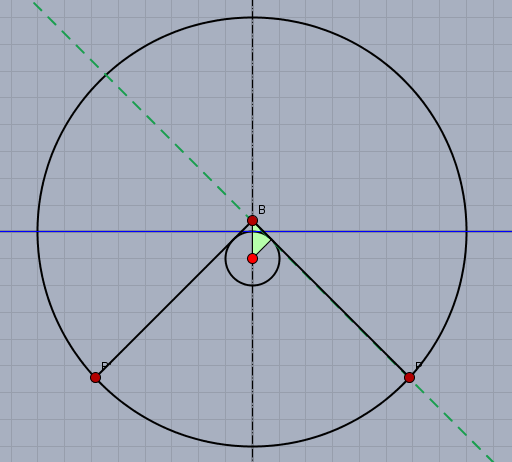
In der Zeichnung siehst Du ein kleines markiertes Dreieck. Es ist rechtwinklig und gleichschenklig. Folglich liegt der Punkt \(B\) bei \(b_y=R(\sqrt 2 - 1)\) und die Gerade (grün markiert) hat die Steigung \(y'=-1\). Demnach ist ihre Funktion $$y = -x + R(\sqrt 2 -1)$$setzte dies in die Kreisgleichung ein$$x^2 + \left( -x + R(\sqrt 2 - 1)\right)^2 = \left( \frac D2 \right)^2$$ und berechne das \(x\). Das \(x\), welches \(\gt 0\) ist, ist das gesuchte. Einsetzen in die Funktion für die Gerade gibt das gesuchte \(y\).
Ich bekomme als Ergebnis:$$\begin{aligned}x &= 5\left( \sqrt 2 - 1 + \sqrt{ 29 + 2\sqrt 2 }\right) \approx 30,28\\ y &= -x + 10(\sqrt 2 -1) \approx -26,14\end{aligned}$$Das \(y\) ist negativ, da es im Koordinatensystem im negativen Bereich liegt.
Gruß Werner