http://www.rither.de/a/mathematik/analysis/differentialrechnung/tangente-an-punkt-im-graphen/
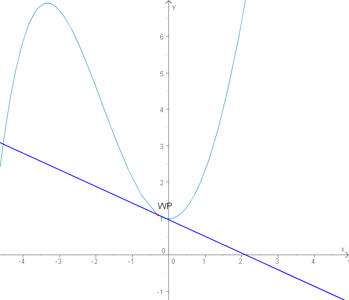
du siehst dort den dunkelblauen strich, das ist die tangente in einem punkt. dein stift soll dieser blaue strich an deinem graphen sein mit dem anfangspunkt (-2;-8). in diesem punkt ist der stift ziemlich steil, nahezu senkrecht. dann solllst du mit dem stift entlang des graphen richtung (2;8) wandern und zwar so, dass dein stift in jedem punkt eine tangente darstellt. dabei stellst du fest, wie sich die lage des stifts ändert, dass er langsam in die waagerechte position, dann irgendwann immer schneller in die waagerechte position übergeht, um dann wieder immer steiler zu werden ...
die 'steilheit' deines stiftes entspricht der ersten ableitung.
"und mit der Ableitungsfunktion f kann ich nichts anfangen.."
die ableitungsfunktion f´(x)=3x2 liefert dir für jedes x die steigung der tangente im punkt x des gaphen f(x) = x3
"Wie macht man die Ableitungswerte?"
indem du für x eine zahl in die ableitungsfunktion einsetzt.
dann müsstest du so etwas wie steiler stift -> großer ableitungswert, flacher stift -> kleiner ableitungswert erkennen.