Hallo Anton,
das Thema ist irgendwie interessant! Zunächst mal eine konkrete Zeichnung:

Die rote Kurve zeigt die Länge von \(s\) in Abhängigkeit von \(x\). Das Maximum für \(s\) liegt offensichtlich in der Nähe von \(0,7\).
Man kann das ganze auch verallgemeinern. Für eine beliebige Funktion \(f(x)\), auf dessen Graphen sich der Punkt \(A\) des Dreiecks befinden soll.
Ich habe als erstes den Mittelpunkt von A und B berechnet, um auf die Höhe des Dreiecks zu kommen.
Nun - die Höhe \(h\) des Dreiecks ist doch schlicht \(f(x)\). Und für den Fall oben in Deiner Frage wäre \(f(x)=\frac 1x\)
Habe mir gedacht, dass c=2x ist ...
So ist es. Setzt man das in die Gleichung für \(s\) ein, so erhält man \(s\) in Abhängigkeit von \(x\):$$s(x) = \frac{2xh}{h + 2x}$$Jetzt könnte man natürlich auch \(h=f(x)\) einsetzen und nach \(x\) ableiten und 0 setzen, um das Optimum für \(s\) zu bestimmen. Das habe ich auch gemacht, und mich dabei so verrechnet, dass ich hier ein falsches Ergebnis hingeschrieben hatte.
Aber es gibt ja noch den Lagrange Multiplikator. Du hattest hier gefragt, wann man damit Zeit (bzw. Aufwand) einspart. Und hier habe ich auf jeden Fall Zeit und Aufwand gespart, da ich damit schneller und sicherer zum Ergebnis gekommen bin. Ich setze \(f(x)-h=0\) als Nebenbedingung:$$L(x,h,\lambda) = \frac{2xh}{h + 2x} + \lambda(f(x)- h) \\ \frac{\partial L}{\partial h} = \frac{2x(h+2x) - 2xh}{(h+2x)^2}- \lambda = \frac{4x^2}{(h+2x)^2} - \lambda \space \to 0\\ \frac{\partial L}{\partial x} = \frac{2h(h+2x) - 4xh}{(h+2x)^2} + \lambda f'(x) = \frac{2h^2}{(h+2x)^2} + \lambda f'(x) \space \to 0\\ \frac{2h^2}{(h+2x)^2} + \frac{4x^2}{(h+2x)^2} f'(x) = 0 \\ 2h^2 + 4x^2 f'(x) = 0 \\ h^2=-2x^2f'(x) \\ \frac hx = \sqrt{-2 f'(x)}$$Und dieses \(h/x\) ist doch nichts anderes als die Steigung der Geraden durch \(OA\) (s.o.). Und es gibt nur dann eine (reelle) Lösung, wenn \(f'(x) \lt 0\) ist. Das macht ja auch Sinn - wäre die Steigung der Funktion positiv, so würde \(s\) über alle Grenzen wachsen, es gibt also kein lokales Extremum.
Für jede lineare Funktion der Form \(f(x)=b-mx\) mit \(m \gt 0\), wäre $$\frac hx = \sqrt{2m}$$Also in dem Fall von \(f(x)=1-x\) - wie in Aufgabe 4b) - ist dieses Verhältnis \(=\sqrt 2\)
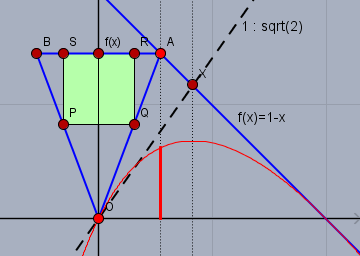
man zieht also vom Ursprung \(O\) einfach eine Gerade mit der Steigung \(\sqrt 2\), die die Funktion \(f(x)=1-x\) im Punkt \(X\) schneidet - der Position des lokalen Extremums für \(s\).
Und was die Funktion \(f(x)=1/x\) betrifft: die Ableitung ist \(f'(x)=-1/x^2\). Einsetzen in die Gleichung oben für \(h/x\) führt zu$$\frac hx = \sqrt{2\frac 1{x^2}} \implies h = \sqrt 2, \space x=\frac 12 \sqrt 2$$
Gruß Werner