Winkel bestimmen im Dreieck. Rheinbrücke

Question

Aufgabe:e)Bestimme den Winkel,den die Seile mit der Fahrbahn einschließen

Problem:Ich kann das nicht,es gehört zum Einstieg Trigonometrie....ich hoffe jemand hilft mir➡Die Bilder sind Material das helfen könnte.....Tut mir leid für den Text unter dem Bild ich denke der ist aber nicht relevant alles sieht man in der zeichung und dem bild...ließ sich nicht vermeiden....Entschuldigung

Answer 1

ich gehe davon aus, dass du die Längen der anderen Halteseile berechnen sollst.

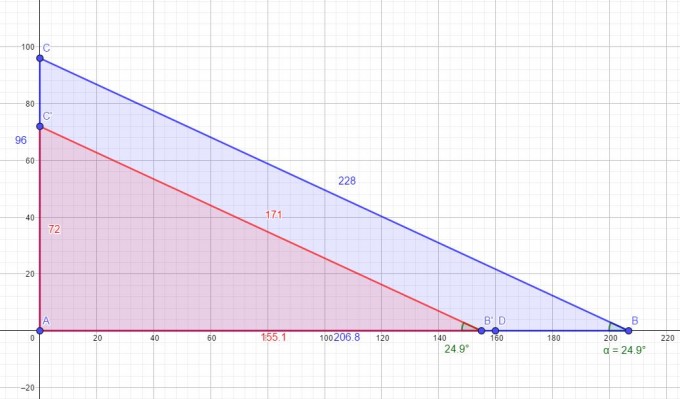
Mit den Angaben aus dem Text sind vom größten der vier Dreiecke (blau)  bekannt: Hypotenuse = 228 m, Ankathete = 96 m. Von den anderen drei Dreiecken kannst du auch die Ankatheten durch die gleichmäßigen Abstände bestimmen.

Der Winkel zwischen Fahrbahn und den Seilen ergibt sich durch

$$sinα=\frac{Gegenkathete}{Hypotenuse}=\frac{96}{228}⇒α=24,9°$$

Der ist für alle vier Dreiecke gleich.

Für das nächste Dreieck (rot)  kannst du mit den Informationen Alpha = 24,9° und der Ankathete = 72 die Hypotenuse ebenfalls mit dem Sinussatz berechnen:

$$Hypotenuse = \frac{72}{sin (24,9)}$$

So gehst du auch zur Berechnung der restlichen beiden Halteseile vor.

Gruß, Silvia

Comments

Hallo Silvia,

Tipp:

Es sieht schöner aus, wenn du \sin und \text{Gegenkathete} verwendest:$$\sin α=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}=\frac{96}{228}⇒α=24,9°$$

---

ich gehe davon aus, dass du die Längen der anderen Halteseile berechnen sollst.

Eigentlich würde mann dann doch nur den Strahlensatz brauchen.

Für das nächste Dreieck (rot)  kannst du mit den Informationen Alpha = 24,9° und der Ankathete = 72 die Hypotenuse ebenfalls mit dem Sinussatz berechnen:

Unterscheide den normalen Sinus vom Sinussatz. Der Sinus gilt in rechtwinkligen Dreiecken. Der Sinussatz gilt in allen Dreiecken.

Man könnte zwar auch den Sinussatz benutzen wobei SIN(90°) zu 1 vereinfacht werden kann, aber nötig ist das nicht.

---

Woher weiß man das man sinus benutzen muss?....und nicht z.b tan oder cos weil man hat ja alle drei längen

---

96 und 228 sind direkt in der Aufgabe gegeben. Mit dem Sinus kannst du es also direkt mit den Angaben die du hast berechnen. Mit dem Tangens oder Cosinus musst du eventuell auf selber berechnete Seiten zurückgreifen, die auch verkehrt berechnet sein können.

Ich versuche es möglichst zu vermeiden mit selbst berechneten Sachen weiterzurechnen, wenn es nicht nötig ist.

---

Es sieht schöner aus, wenn du \sin und \text{Gegenkathete} verwendest:

@Anton OK, du Schöngeist, das mache ich demnächst.

Eigentlich würde mann dann doch nur den Strahlensatz brauchen

@Mathecoach Ja, aber das Thema ist "Einstieg in die Trigonometrie".

Danke für den Hinweis Sinus/Sinussatz.

@darknight  Die ursprünglichen Angaben (228 und 96 m) "fordern" den Sinus.

---

Gibt es auch sin (gamma) und sin (delta) und cos (gamma) cos (gamma)...etc und wofür brquch man die?

---

Es gibt auch den Sinus von gamma, delte, etc. Da du die Winkel so nennen kannst wie du möchtest, könntest du auch

sin(Winkel_den_das_Seil_mit_der_Fahrbahn_einschließt)

bilden. Faule Mathematiker beschränken sich allerdings gerne bei Winkeln auf die griechischen Buchstaben.

Answer 2

Das obere Seil, der Mast und die Fahrbahn bilden ein rechtwinkliges Dreieck.

Die Länge der Hypotenuse beträgt 228 m, und die Länge der Kathete, die dem gesuchten Winkel GEGENÜBER liegt, ist 96 m.

Jetzt kratze mal deine Kenntnisse aus Klasse 9 über das Verhältnis von Gegenkathete und Hypotenuse zusammen.

PS: Wenn ihr das tatsächlich noch nicht hattet, dann zeichne das Dreieck und miss den Winkel.

Comments

Vlt noch ein Tipp kann ich dann evtl Googeln

Answer 3

Der Sinus eines Winkels ist definiert als das Verhältnis von Gegenkathete zu Hypotenuse

SIN(α) = 96/228

α = SIN^{-1}(96/228) = 24.90°