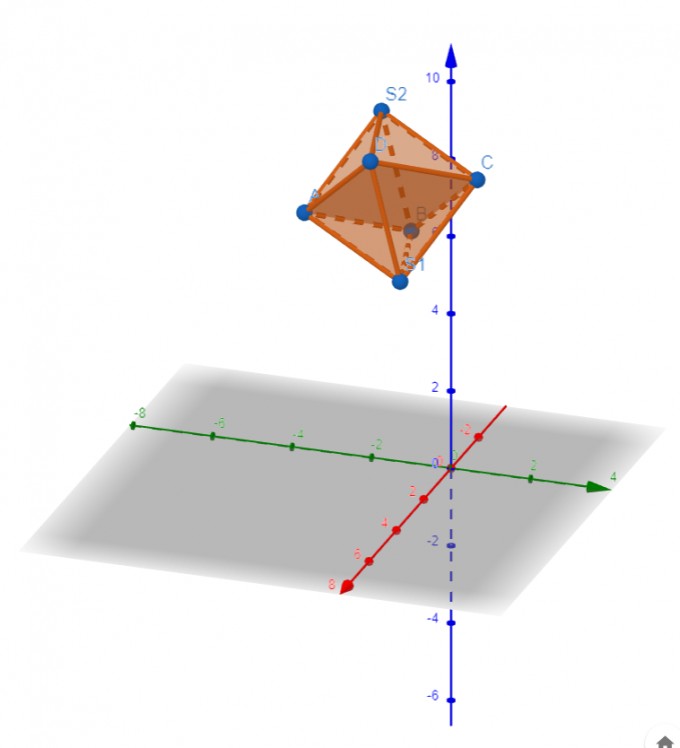
a)
AB = B - A = [0, -1, 6] - [2, -3, 7] = [-2, 2, -1]
AD = D - A = [3, -1, 9] - [2, -3, 7] = [1, 2, 2]
Fußpunkt
F = 1/2·(A + C) = 1/2·([2, -3, 7] + [1, 1, 8]) = [1.5, -1, 7.5]
Normalenvektor
N = AB ⨯ AD = [-2, 2, -1] ⨯ [1, 2, 2] = [6, 3, -6]
Höhenvektor
H = 2.25·[6, 3, -6]/|[6, 3, -6]| = [1.5, 0.75, -1.5]
Spitze
S1 = F + H = [1.5, -1, 7.5] + [1.5, 0.75, -1.5] = [3, -0.25, 6]
S2 = F - H = [1.5, -1, 7.5] - [1.5, 0.75, -1.5] = [0, -1.75, 9]
b)
AS1 = S1 - A = [3, -0.25, 6] - [2, -3, 7] = [1, 2.75, -1]
α = ASIN(AS1·N/(|AS1|·|N|)) = ASIN([1, 2.75, -1]·[6, 3, -6]/(|[1, 2.75, -1]|·|[6, 3, -6]|)) = 46.67°