Vom Rechteck zur Pyramide, Pyramidenvolumen und Spurpunkte berechnen

Question

Es gibt noch einen zweiten Teil, ich bräuchte da auch eure Mathe-Unterstützung!

2. Die Punkte A(4| 2| 3), B(4| 4| 3), C(1| 4| 3) und D(1| 2| 3) bilden ein Rechteck.
a) Bestimmen Sie die Koordinaten der Spitze S so, dass ein gerade, rechteckige Pyramide mit der Höhe 5 LE entsteht.
b) Zeichnen Sie diese in ein kartesisches Koordinatensystem.
c) Berechnen Sie das Volumen der Pyramide. (V=1/3*G*h)
d) Berechnen Sie die Spurpunkte (Durchstoßungspunkte der Koordinatenebenen) der Geraden durch die Punkte A und B.
e) Diskutieren Sie die Lage der Geraden g durch die Punkte A und B und h durch die Punkte S und G(2| 3| 4).

Danke, es grüßt Kati ==)

Answer 1

Hallo Kati,

Bist Du mit Vektoren vertraut? 5 LE, sind das Längs-Einheiten, d.h. ist die Pyramide 5 mal so hoch wie eine Länge ist?

Du könntest bei a) den Mittelpunkt einer Diagonale bestimmen, dann 2 senkrecht zueinander stehende Vektoren der Rechteck-Seiten nehmen und das Vektorprodukt bilden. Dieses auf 5 LE verlängern und zum Mittelpunkt addieren. Dann erhältst Du die Spitze.

LG

Answer 2

"2. Die Punkte A(4| 2| 3), B(4| 4| 3), C(1| 4| 3) und D(1| 2| 3) bilden ein Rechteck."

Korrekt :)

a) Bestimmen Sie die Koordinaten der Spitze S so, dass ein gerade, rechteckige Pyramide mit der Höhe 5 LE entsteht.

Einfach den Mittelwert von gegenüberliegenden Punkten bilden für x und y, für z eine der z-Komponenten (alle haben den Wert 3) mit 5 LE addieren.

x = (4 + 1)/2 = 2,5
y = (2 + 4)/2 = 3
z = 3 + 5 = 8

P(2,5|3|8)

b) Zeichnen Sie diese in ein kartesisches Koordinatensystem.

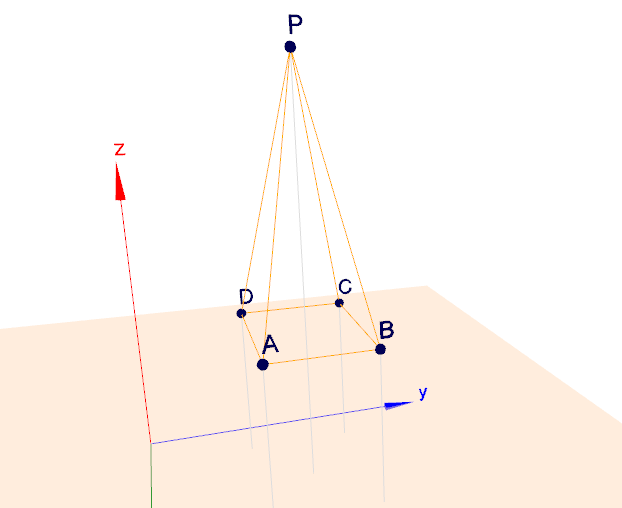
Die 3D-Zeichnung kannst du online mit dem Geoknecht anpassen.

c) Berechnen Sie das Volumen der Pyramide. (V=1/3*G*h)

G = 3 * 2 = 6 FE
h = 5

V = 1/3 *G*h = 1/3 * 6*5 = 10 (richtig, siehe Pyramidenrechner)

d) Berechnen Sie die Spurpunkte (Durchstoßungspunkte der Koordinatenebenen) der Geraden durch die Punkte A und B.

Gerade AB hat die Geradengleichung: g: (x|y|z) = (4|2|3) + r·(0|2|0)

Spurpunkt ist: v_xz = (4|0|3) 

e) Diskutieren Sie die Lage der Geraden g durch die Punkte A und B und der Geraden h durch die Punkte S und G(2| 3| 4).

Ich vermute, S soll hier der ermittelte Spurpunkt sein? Dann sieht die Grafik der Geraden so aus: 

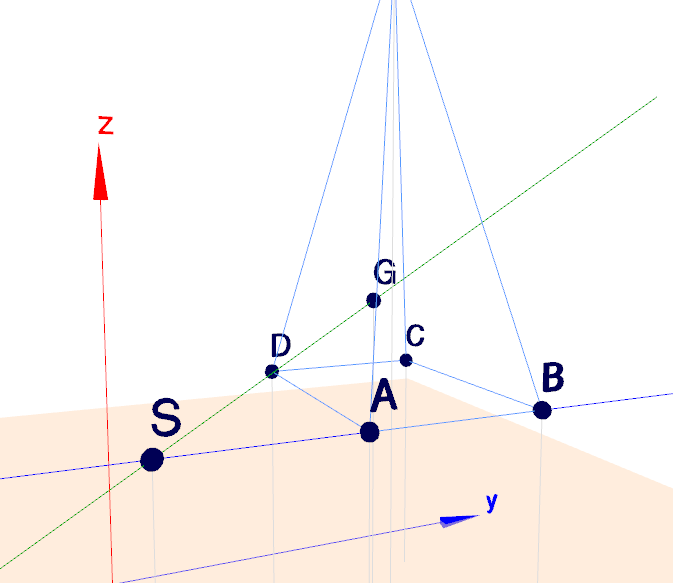
Offensichtlich schneiden sich beide Geraden im Punkt S.