Funktionsuntersuchungen

Question

Aufgabe:

Bestimmen Sie rechnerisch alle Extrempunkte des Graphen von f. Skizzieren Sie anschliessend den groben Verlauf des Graphen von f mithilfe dieser Information und entscheiden Sie jeweils ,ob es sich um ein lokales oder globales Extremum handelt .

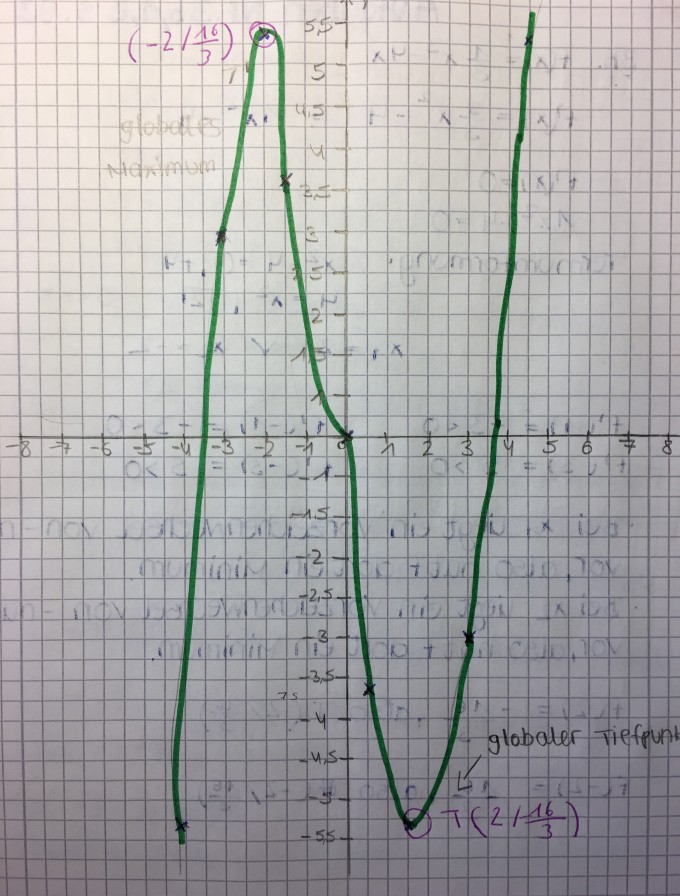
b) f(x)= 1/3 x^3 -4x

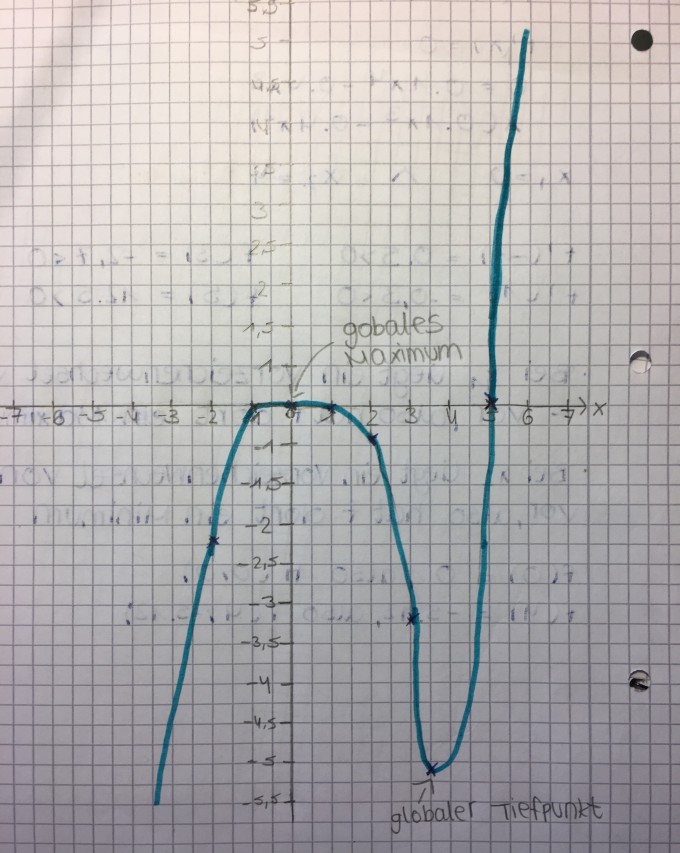
d) f(x)=-0.5x^4 + 2x^3 -2x^2

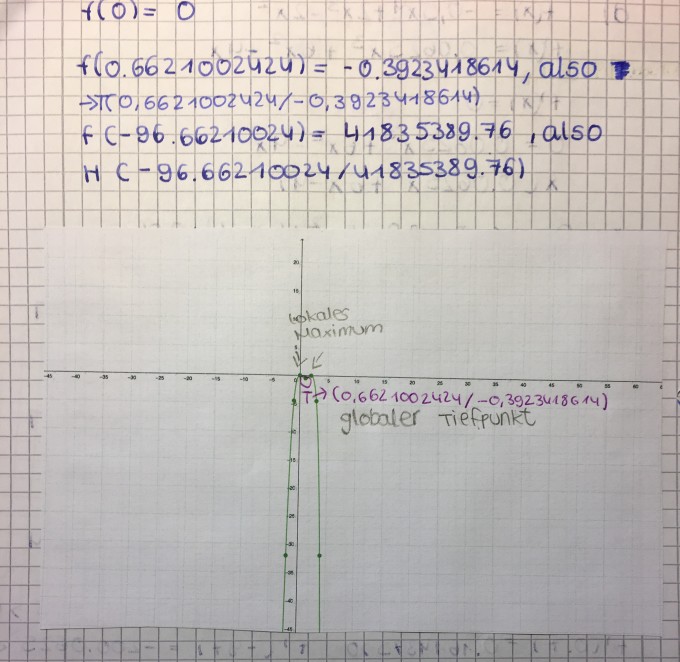
e) f(x)=0.02x^5-0.1x^4
Problem/Ansatz:

Wollte fragen ,ob meine Ergebnisse richtig sind.Habe bei der Nr.3b ein Problem bei dem Bestimmen des Vorzeichenwechsel an der Nulle x2=-2 .Bei mir kommt da ein Tiefpunkt raus, obwohl da ein Hochpunkt sein muss.

Answer 1

b) f(x)= 1/3 x³ -4x

richig ist x₁=2   x₂=-2.

Dann ist f(x₁)=f(2)=8/3-8=-16/3 und f(x₂)=f(-2)=-8/3+8=16/3

Answer 2

Hallo

 -3 ist kleiner als -1 also f'(-3)=5, f'(-1)=-3 also Vorzeichenwechsel von + nach - also Max!

ausserdem die funktion ist da nur ungerade Exponenten vorkommen punktsymmetrisch zum 0 Punkt, d.h. wenn rechts ein min ist ist links ein Max. weder ds max noch das Min sind global da der Graph  ja für große x größer als das max und für kleine x kleiner als das min ist.

globaler TP heisst es gibt auf dem Graphen keinen tieferen Punkt, entsprechend für globaler Hochpunkt, die Teile musst du also korrigieren! sonst ist alles ok.

Gruß lul

Answer 3

f(x)= 1/3 x^3 -4x
f ´( x ) = x^2 - 4
f ´´( x ) = 2x

Extrempunkte
x^2 = 4
x = 2
x = -2

Eingesetzt in die 2.Ableitung

f´´ ( 2 ) = 4
Linkskrümmung : der Punkt ist ein Tiefpunkt
f´´ ( -2 ) = -4
Rechtskrümmung : der Punkt ist ein Hochpunkt