Aufgabe : Zeigen Sie mit Hilfe der Transformationsformel, dass :
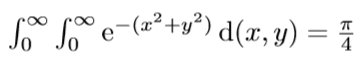
was ich gemacht habe ist , dass ich die Polarkoordinaten statt kartesischen Koordinaten verwendet habe und kam auf
\( \int\limits_{}^{\ } \) \( \int\limits_{}^{\ } \) \( e^{-r²} \)r dφdr mein Problem war aber die Auswahl der Grenzen ! nach mehreren Versuchen habe ich einfach \( \int\limits_{0}^{\infty} \) \( \int\limits_{0}^{\ (π/2) } \) probiert und es hat geklappt also kam das richtige raus aber die Frage ist wieso ? also warum sollte man die Grenzen so auswählen ? Die machen mir nämlich keinen Sinn ^^ ! ich dachte es wäre sowas wie \( \int\limits_{0}^{\infty} \) \( \int\limits_{0}^{\ 2π } \)
ich hoffe mir könnte einer helfen , weil ich treffe echt Schwierigkeiten mit sowas !