Extremwertaufgabe. Flächeninhalt des Aluminiumstreifens soll maximal werden.

Question

Aufgabe:

Kann mir jemand diese Extremwertaufgabe erklären?

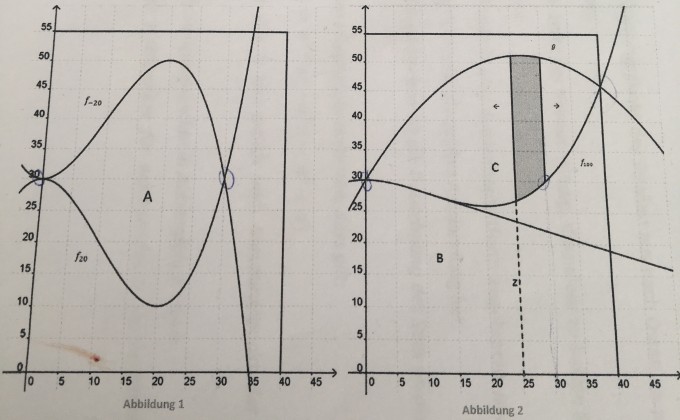
Der Graph der Funktion f100 beschreibt die untere Schnittkante des Holzteils C. Die obere Schnittkante des Holzteils C ist Teil einer nach unten geöffneten Parabel g mit g(x)= -3/100*x^2+ 8/5*x+30

Auf Holzteil C soll ein 5cm breiter Aluminiumstreifen parallel zur yAchse aufgeschraubt werden.

Der Flächeninhalt des Aluminiumstreifens soll maximal werden.

1) Ermitteln Sie rechnerisch den maximalen Flächeninhalt

2) Bestimmen sie den Abstand des Aluminiumstreifens von der y Achse.

Nachtrag:

f_100(x):= (1/1000)x^3-(3/100)x^2+30

Problem/Ansatz:

Ich verstehe leider die ganze Aufgabe nicht und auch Ansätze helfen mir nicht wäre nett wenn es mir jemand erklären bzw. zeigen kann wie es geht. von a-d habe ich alles geschafft nur e nicht.

Comments

Was ist \( f_{100} \)?

---

(1/1000)x^3-(3/100)x^2+30

Answer 1

Du solltest mind. noch f100(x) angeben.

EDIT: Antwort mit f100(x) in einem Kommentar.

Comments

Vorschlag :

a(x)  =  49/480*x^2 - 125/6
b(x)  =  1/64*x^2 + 1,5x - 6,25

f_k(x)  =  a(k)*(x/k)^3 - b(k)*(x/k)^2 + 30

---

(1/1000)x^3-(3/100)x^2+30

---

d(x) = (-3/100·x^2 + 8/5·x + 30) - (1/1000·x^3 - 3/100·x^2 + 30) = 1.6·x - 0.001·x^3

A(a) = ∫ (a bis a + 5) (1.6·x - 0.001·x^3) dx = -0.005·a^3 - 0.0375·a^2 + 7.875·a + 19.84375

A'(a) = - 0.015·a^2 - 0.075·a + 7.875 = 0 --> a = 20.55 cm

A(20.55) = 122.4 cm²

Answer 2

Hallo

 die Fläche des Alus ist doch von einem unbekannten x1 bis x1+5 zwischen den 2 Kurven, also das Integral von x1 bis x1+5 von der Differenz Parabel - Kurve.

davon das max in Abhängigkeit. von x1

Gruß lul

Comments

(1/1000)x^3-(3/100)x^2+30  Das ist f100(x) 

Und trotz des Ansatzes verstehe ich es nicht. Also ich komm nicht auf den x Wert alle meine Rechnungen sind falsch :(

Answer 3

Hi,

sei \( g(x) = -\frac{3}{100} x^2 + \frac{8}{5} \)  und \( f_{100}(x) = \frac{1}{1000} x^3 - \frac{3}{100} x^2 +30 \), dann ist folgendes zu maximieren

$$ F(x) = \int_x^{x+5} (g(s) - f(s) ) ds $$

Es gilt $$ \frac{d}{dx} F(x) = g(x+5) - f(x+5) - g(x) + f(x) = -\frac{3}{200} x^2  -\frac{3}{40}x +\frac{63}{8} $$

Hiervon die Nullstellen bestimmen ergibt \( x_{1,2} = - \frac{5}{2} \pm \frac{5}{2} \sqrt{85} \)

Über die zweite Ableitung sieht man, dass nur \( x_1 \) das Maximum ergibt.

Die Fläche ist dann \( F(x_1) = 122.447 \)

Comments

Warum ist F(x)= g(x+5)-f(x+5)-g(x). ??

Also wie komme ich auf die stammfunktion verstehe ich nicht

---

Siehe https://de.wikipedia.org/wiki/Fundamentalsatz_der_Analysis