Hallo limonade,
(1) Weil \(0 \ne 3\) eine nicht-wahre Aussage ist, haben die drei Gleichungen keinen gemeinsamen Schnittpunkt.
Gleichungen haben natürlich keinen Schnittpunkt, aber ein System von zwei linearen Gleichungen mit zwei Unbekannten kann auch als zwei Geraden in der Ebene aufgefasst werden
(2) Bei einer 2x2 Matrix weiß ich, dass die zwei Gleichungen in so einem Fall keinen Schnittpunkt haben.
Du hast drei Gleichungen, was drei Geraden in der Ebene entspricht, aber nur zwei Unbekannte \(x_1\) und \(x_2\). D.h. das Gleichungssystem ist überbestimmt. Somit ist jede einzelne der drei Gleichungen entweder redundant zu den beiden anderen oder ein Widerspruch (hier letzteres).
~plot~ x-1;(9-x)/3;2-x;{3|2};{-1,5|3,5};{1,5|0,5} ~plot~
Ich habe die drei Gleichungen als Geraden dargestellt. Jeweils ein Paar der Geraden hat einen Schnittpunkt, aber es gibt keinen gemeinsamen für alle drei. Es ist also nicht so, dass Du keinen(!) Schnittpunkt hat; das System ist lediglich überbestimmt.
(3) Was weiß ich aber bei einer Matrix der Grösse \(n \times n \) für \(n\ge3\) ?
Wen eine \(n \times n\)-Matrix vorliegt, deren Determinante \(\ne 0\) ist, und keine \(n \times m\)-Matrix(!), so wirst Du immer eine eindeutige Lösung erhalten, also eine Menge von \(n\) Zahlen, die alle Gleichungen erfüllen. Ist die Determinante \(=0\) so gibt es entweder keine oder unendlich viele Lösungen.
(4) Welche dieser Gleichungen haben keinen gemeinsamen Schnittpunkt ? Es ist ja möglich, dass die erste und die zweite Gleichung eine Lösung (gem. Schnittpunkt) besitzen aber die dritte und die erste dafür nicht.
Siehe oben! Jedes Paar der Gleichungen hat eine Lösung, bzw. jedes Paar von Geraden hat einen eindeutigen Schnittpunkt.
(5) Wie ist diese Matrix nach Gauß zu interpretieren, also was lese ich genau hier aus dem Gauß?
Sehr gute Frage! mache den Gauß noch fertig, addiere die zweite Zeile noch zur ersten; so erhältst Du$$\left( \begin{array}{cc|c} 1 & 0 & \colorbox{#ffff00}{3} \\ 0 & 1 & \colorbox{#ffff00}{2} \\ 0 & 0 & -3 \end{array} \right)$$Du hast nach den ersten beiden Gleichungen aufgelöst, also steht rechts in den ersten beiden Zeilen der Schnittpunkt \((3|2)\) der ersten beiden Geraden (blau und rot).
Für die dritte Gleichung führe ich eine dritte Koordinate hinzu:$$\begin{aligned} x_1 - x_2 + 0 &= 1 \\ x_1 + 3x_2 + 0 &= 9 \\ x_1 + x_2 + \colorbox{#ffff00}{$x_3$} &= 2\end{aligned}$$Das ist natürlich willkürlich gewählt, soll auch nur zeigen, wie die Zusammenhänge sind. Eine dritte Koordinate \(x_3\) ist auch eine dritte Dimension. Wir haben jetzt also keine Geraden in der Ebene, sondern Ebenen im Raum vor uns:
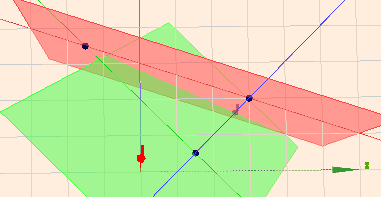
Betrachtet man nur die XY-Ebene, so hat sich nichts geändert. Es sind wieder drei Geraden mit den drei gleichen Schnittpunkten. Klick auf das Bild und drehe die Szene. Durch das Einfügen von \(x_3\) 'kippt' die dritte (grüne) Ebene etwas und es gibt eine Punkt \(P=(3|2|-3)\) außerhalb der XY-Ebene, deren Koordinaten jetzt alle drei Gleichungen erfüllen.
Gruß Werner