Betrachte die gesamte Trittfläche einer Stufe

Question

Aufgabe:

Betrachte die gesamte trittfläche einer stufe

a. Zeichne diese Trittfläche im Maßstab 1:10

b. Berechne die Trittfläche einer Stufe

c.Berechne das Volumen einer Stufe

Problem/Ansatz:

Eine stufe ist 80 cm lang, 18 cm hoch und hat eine Außenbreite von 30cm

Genau 12 Stufen ergeben eine vollständige drehung (360°)

Alle stufen sind gleich

Comments

Stimmen die eingezeichneten 30 cm, so ist mit Überlappungen der Bretter zu rechnen (?)

---

Da haben wohl meine fetten finger die 3 getroffen. Tut mir leid an alle.

Die richtige länge ist 20 cm und nicht 30.

Nochmals tut mir leid.

Mfg

---

Du hast allerdings in der Skizze auch 30 cm hingeschrieben.

---

Oh ich dachte sie meinen die mittel säule.

Ja die Bretter sind 30cm und überlappen sich

---

Hallo Karima,

Deine Angaben widersprechen sich

Ja die Bretter sind 30cm und überlappen sich

Zeichne ich alles auf, so ergibt sich folgendes Bild:

Mit einem Außenradius von $80\text{cm} + 30\text{cm}/2 = 95\text{cm}$ und einer Länge der Sehne (rot) von $30\text{cm}$ ergibt sich ein Zentriwinkel der Stufe von ca. $18.2°$. Das ist deutlich weniger als die Teilung von $360°/12=30°$ (blau).

So liegt keine Überlappung vor!

Gruß Werner

---

Dann hab ich und mein mathe partner was falsch erechnet. Die länge 30cm hat er so erechnet

Da 12 stufen 360° sind

Hat er 360 ÷ 12 = 30 gerechnet.

Ich dachte mir das da was nicht stimmen kann wegen der überlappung auf den zeichnungen.

Wenn sie wollen, kann ich ihnen die vorherigen aufgaben schicken.

Mfg

Karima

---

Hat er 360 ÷ 12 = 30 gerechnet.

Diese $30$ sind keine $30\text{cm}$, sondern $30°$ - also ein Winkel und keine Länge. Die $360°$ sind ja auch ein Winkel.

Tipp: ein Teil eines Winkels ist immer ein Winkel, genau wie z.B. ein Anteil aus einer Geldsumme immer eine Summe Geldes ist und keine Länge oder was anderes.

Wenn sie wollen, kann ich ihnen die vorherigen aufgaben schicken.

Ja - für den Aufgabeteil (c) (Berechnung des Volumens) ist noch eine weitere Angabe notwendig. Entweder ein Breitenmaß, der Zentriwinkel der Stufe oder ein Maß für die Überlappung.

---

Hier sind die aufgaben von 1-5 

Aufgabenstellung:

In einem runden Aussichtsturm befindet sich eine Wendeltreppe, die von ganz unten bis zur Aussichtsplatform ins Freie führt. Der Turm und die Treppe werden in den Skizzen Vereinfacht.

Der Turm hat folgende Maße 

-Die Aussenwand des Turms ist 30 cm dick.

-Genau 12 Stufen ergeben zusammen eine vollständige Drehung (360°)

-Jede stufe ist 18cm hoch; alle stufen haben die gleichen Maße.

-Die Aussichtsplatform befindet sich 16,20 m über dem Boden des Erdgeschosses und wird von einem Geländer begrenzt.

-Weitere maße sind aus der Skizze zu ersehen

Skizze 1:

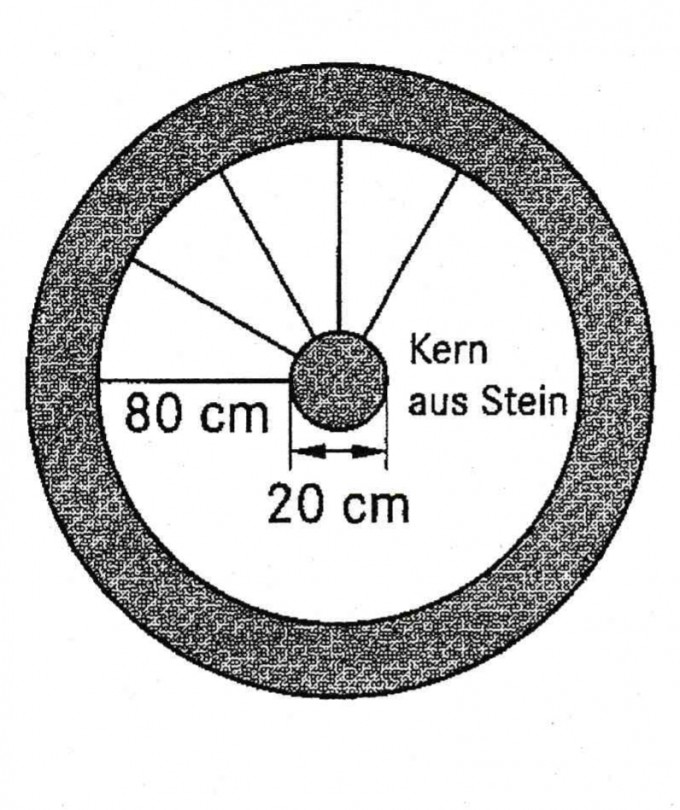
Aufgaben:

1. Gib den äußeren Umfang des Turms an.

2. Die Außenmauer des fensterlosen Turms soll gestrichen werden. Berechne die zu streichende Fläche.

Aufgaben 2:

Skizze 2 

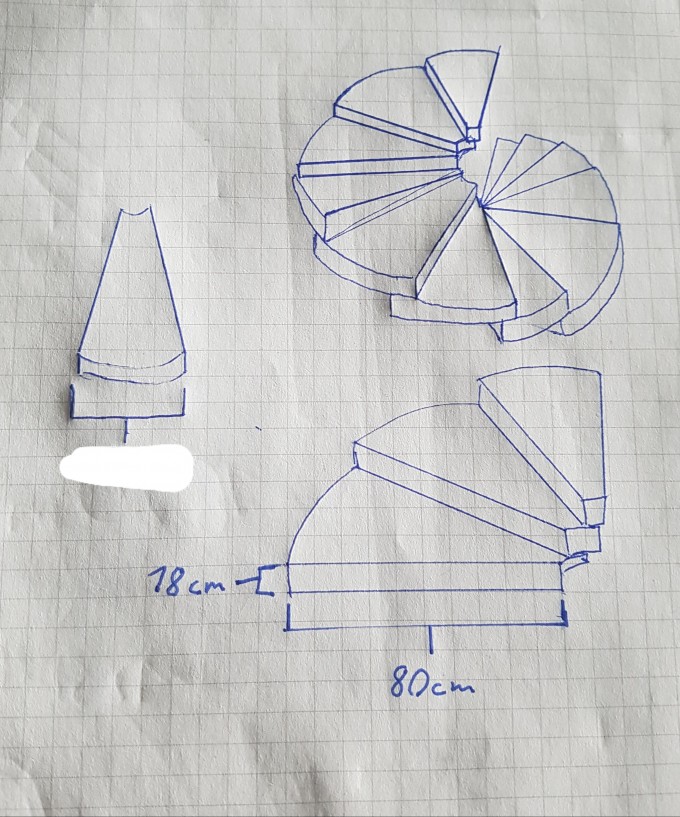
3. Wieviel Stufen hat die Treppe Insgesamt?

4. Herr Mustermann ist 2,02 meter groß. Kann er auf der treppe aufrecht stehen, ohne mit dem kopf an die Stufe über sich zu stoßen?

5. Betrachte die gesamte Trittfläche einer stufe

a. Zeichne diese Trittfläche im Maßtab 1:10

b. Berechne die trittfläche einer Stufe.

c. Berechne das Volumen einer stufe.

So, das sind alle Aufgaben einmal aufgeschrieben. Danke das sie sich damit befaßen und mir helfen

Mfg.

Karima

Answer 1

Hallo Karima,

da hast Du ja einiges durcheinander geworfen. Der innere Radius ist $r_i = 10 \text{cm}$ und nicht 15cm(!). Der Innenradius des Turms bzw. Außenradius der (Wendel)Treppe ist $r_w=(80 + 20/2)\text{cm} = 90\text{cm}$ und der Außenradius des Turms ist $r_a = r_w + 30 \text{cm} = 120 \text{cm}$. Damit ist der Außenumfang $U_a$ des Turms

$$U_a = 2 \pi \cdot r_a = 2 \pi \cdot 120 \text{cm} \approx 754,0 \text{cm}$$

Ist $h=16,2\text{m}$ die Höhe des Turms, dann ist die Außenfläche $O_a$:

$$O_a = U_a \cdot h = \pi \cdot 2,4 \text{m} \cdot 16,2 \text{m} \approx 124,4 \text{m}^2$$

Ist $h_{st}=18\text{cm}$ die Höhe einer Stufe und $h=16,2\text{m}$ die Gesamthöhe der Treppe (gleich der Turmhöhe), so ist die Anzahl $n_{st}$ der Stufen:

$$n_{st} = \frac {h}{h_{st}} = \frac{16,2 \text{m}}{0,18 \text{m}} = 90$$

Die Trittfläche $A$ einer Stufe ist ein 12'tel der Differenz des Kreises der Wendeltreppe minus den Teil, der durch Kern eingenommen wird.

$$A = \frac 1{12} \left( \pi r_a^2 - \pi r_i^2\right) \approx 20,94 \text{dm}^2$$

Beim Volumen gehe ich davon aus, dass keine Überlappung existiert (es ist keine Angabe dazu vorhanden). Dann ist

$$V_{st}=A \cdot h_{st} \approx 37,7 \text{dm}^3$$

... und ein Geoknecht3D-Bild als Goodie:

(klick auf das Bild)

Gruß Werner

Answer 2

A=1/12*π*(95²-15²)≈2303,83cm²

V=A*h=2303,83cm²*18cm≈41469 cm³

Comments

Die Löschung meines Beitrags macht die Antwort nicht besser.

---

Kannst du erkennen, wie breit die Überlappungen sein sollen?

---

Das kannst du mit dem Sinus berechnen.

Answer 3

Betrachte die gesamte trittfläche einer stufe

a. Zeichne diese Trittfläche im Maßstab 1:10

Wenn ich die Überlappungen richtig verstanden habe, ist das ein Kreissektor mit Zentriwinkel 30°.

b. Berechne die Trittfläche einer Stufe

Wenn ich das richtig verstanden habe:

A = 1/12 * Kreisfläche

A = 1/12 * 80² π cm²

A ≈ 1675.51 cm² 

Eine stufe ist 80 cm lang, 18 cm hoch und hat eine Außenbreite von 30cm

Genau 12 Stufen ergeben eine vollständige drehung (360°)

Answer 4

Die Mittelsäule wird nicht genannt. Daher nehme ich hier den Radius r_i=0. Trittfläche T=π·80²/12. Volumen V=18·T.

Comments

Die Säule hat eine Durchmesser von 30cm

---

Heisst das: Die Wendeltreppe ist von oben gesehen ein Kreis mit Radius 95cm und mit einem Loch mit Radius 15 cm?

Dann kannst du die Trittfläche einer Stufen berechnen als

A = 1/12 * (grosser Kreis MINUS kleiner Kreis)