Komplexe Zahlenebene: Skizziere die folgenden Mengen in der Komplexen Zahlenebene

Question

wie meine Überschrift schon sagt muss ich Mengen in ein Komplexes Zahlensystem einskizzieren.

Meine Frage bzw. Fragen sind:

-Was bedeuten die Betragsstriche? Was verändert sich dadurch wenn keine vorhanden wären?

-Und wie soll ich anfangen auf was will ich hinaus??

Und hier die Aufgaben:

A) { z ∈C | |z-1-i > 2}

B) { z ∈ C | Re(z⁴) = Re(z)⁴

C) { ( -(√3)/2 + i/2)⁴

Bitte helft mir versetehe das echt nicht so.... :(

Danke schon mal

Comments

kann das sein, dass bei A) ein betragsstrich fehlt?

der betrag einer komplexen zahl ist einfach nur die länge des zeigers der zahl in der komplexen ebene.

falls du aber den strich in der mengendefinition meinst, wie z.b. in

{ z ∈ C | Re(z⁴) = Re(z)⁴ },

das ist kein betragsstrich.

---

Ja danke der fehlt... ok!

Und wie berechne ich dass jetzt damit ich das einzeichnen kann?

---

.oO dafür müsste man wissen, wo der betragsstrich fehlt.

hier ?|z-1| -i > 2

oder dort? |z-1-i| > 2

oder an ganz einem anderen ort? :O

---

sorry,

|z-1-i| > 2

---

okay, damit kann ich was anfangen :-)

mach doch schon mal C)

wandle z = -(√3)/2 + i/2 in polarform um z = re^jφ

und dann potenziere z⁴ = (re^jφ)⁴

ich gucke mir solange A) und B) an, muss aber zwischendurch mal was zu essen machen ...

---

Ja ok. Mach das :D

Aber da hängts schon bei der Polarform muss ich gestehen...

---

sorry, hat etwas gedauert ...

... da hängts?
hmm, hast du kein lehrbuch, wo das vernünftig erklärt wird?
das können wir hier jetzt nicht alles nachholen :(

eventuell nur in groben umreißen: es gibt 3 darstellungsformen einer komplexen zahl, rest siehe antwort.

---

die antwort kann ich nicht mehr ändern, also muss ich hier weiter schreiben.

B)

z = x + iy
Re(z)^4 = x^4
Re(z^4) = Re(z)^4
Re((x + iy)^4) = Re(z)^4 = x^4
das geht nur, wenn iy = 0 ist.
dann ist aber z = x + iy = x + 0 = x,
also z = x.
z ist die reelle achse.


A) folgt später ...

:-)

Answer 1

1.

kartesische(oder auch algebraische) form: z = x + iy
z besteht aus der reellen zahl x, dem realteil und aus der imaginären zahl iy, dem imaginärteil.

die bezeichnung kartesische form kommt daher, dass real- und imaginärteil die kartesischen koordinaten der zahl sind, wenn man sie als punkt in der gaußschen ebene darstellt.
die bezeichnung algebraische form kommt daher, dass z als algebraische summe einer rellen zahl und einer imaginären zahl aufgefasst werden kann, eben z = x + iy.

2.
trigonometrische form:

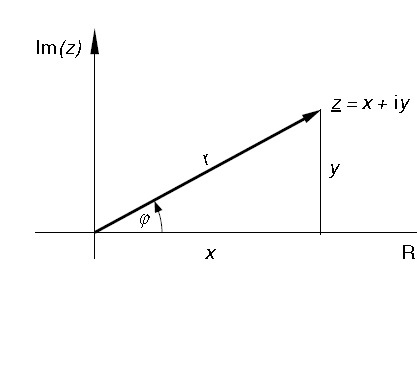
x = r•cos φ, y = r•sin φ (siehe bild)
z = x + i•y = r•cos φ + i•r•sin φ = r(cos φ + i•sin φ)
damit ist die zahl z durch ihre polarkoordinaten r und φ festgelegt.
r: betrag von z

r = √(x²+y²)   (satz des pythagoras)

φ: winkel, phase, oder argument von z
φ = arc tan(y/x)  (quadranten beachten!)

die bezeichnung trigonometrische form kommt daher, dass die trigonometrischen
funktionen sinus und kosinus vorkommen.

3.
exponentialform:
e^iφ = cos φ + i•sin φ das ist die formel von euler.
die muss man sich einfach merken!
wenn du wissen willst, wie sie zustande kommt:
die eulerform bekommt man am einfachsten aus der mac laurinschen reihe von e^x.
siehe entsprechende fachliteratur.

z = r(cos φ + i•sin φ) = r•e^iφ mit (e^iφ = cos φ + i•sin φ)
auch hier sind
r: betrag von z
φ: winkel, phase, oder argument von z

weil die komplexe zahl z in der trigonometrischen und auch in der exponentialform
von polarkoordinaten bestimmt wird, heißen die beiden darstellungsformen auch polarform.

das ganze noch einmal in koprimierter kurzfassung:

z = x + iy = r(cos φ + i•sin φ) = r•e^iφ

r = √(x²+y²)

φ = arc tan(y/x)

damit lassen sich die 3 darstellungsformen eineinander umrechenen.

jetzt können wir endlich z = -(√3)/2 + i/2 in die exponentialform umrechnen! :-)
x = -(√3)/2
y = 1/2

berechnung des winkels φ:

arc tan(y/x) = arc tan ( (1/2) : (-(√3)/2) ) = arc tan ( (1/2) • (2/-(√3)) )
arc arc tan (-1/√3)  = -π/6

φ = π + -π/6, weil z im zweiten quadranten liegt!
φ = 5π/6 (das sind 150°)
betrag:
|z| = r = √( (-(√3)/2)² + (1/2)²) = √( (-(√3)+1)²/4 ) = √(3+1)/2 = 1

damit bekommen wir für z:
z = -(√3)/2 + i/2 = 1•(cos 5π/6 + i•sin 5π/6) = 1•ei5π/6 = ei5π/6

jetzt können wir z potenzieren:
z4 = (rei5π/6)4 = rei(4•5π)/6 = rei20π/6
damit wir z4 in der gaußschen ebene skizzieren können, brauchen wir wieder die
kartesische form.
also wandeln wir die zahl wieder um:
z4 = ei20π/6 = (cos 20π/6 + i•sin 20π/6) = x + i•y
x = cos 20π/6 = -0,5
y = sin 20π/6 = -0,866
z4 = ei20π/6 = (cos 20π/6 + i•sin 20π/6) = -0,5 + -i•0,866

weil der der betrag von z gleich 1 ist, haben wir geometrisch betrachtet den zeiger
der komplexen zahl lediglich um 60° nach links gedreht.

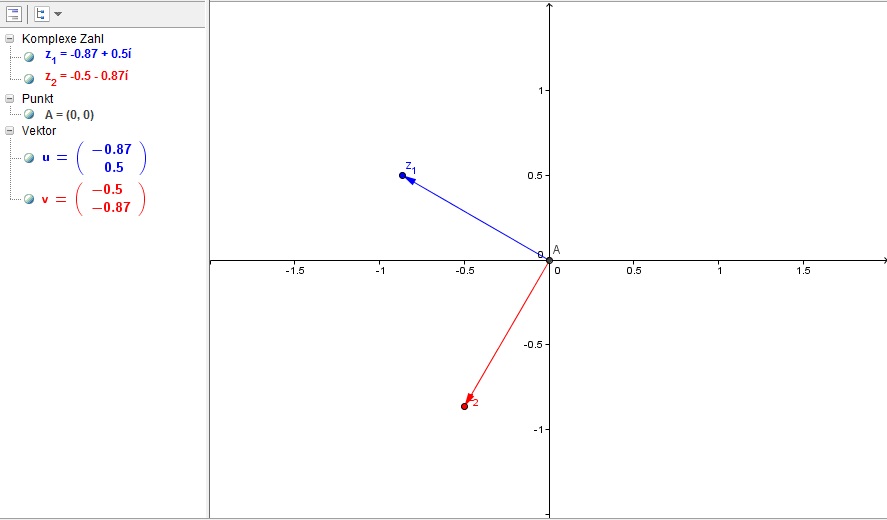
rot ist der potenzierte zeiger.

das wäre teil C) :-)
 

Comments

Vieeeeeeeeeellleennn Dank !!! auch für die mühe :D

---

gern geschehen! :-)

fehlt noch

A)

|z-1-i| > 2

fallunterscheidung

1)
z-1-i ≥ 0 ⇒ |z-1-i| = z-1-i

in worten: wenn z-1-i größer oder gleich 0 ist, dann ist
der betrag von z-1-i gleich z-1-i

2)
z-1-i < 0 ⇒ |z-1-i| = -(z-1-i) = -z+1+i

in worten: wenn z-1-i kleiner 0 ist, dann ist
der betrag von z-1-i gleich -(z-1-i) was dasselbe wie -z+1+i ist.
___________________________________________________________________
wir betrachten den ersten fall

1)

|z-1-i| = z-1-i

z-1-i > 2
z-(1+i) > 2
z > 2 + (1+i)
z > 3 + i
Re(z) + Im(z) > 3 + i

2)

|z-1-i| = -z+1+i

-z+1+i > 2
-z+(1+i) > 2
-z > 2-(1+i)
-z > 1-i
z < -1+i
Re(z) + Im(z) < -1 + i

Re(z) > 3, Re(z) < -1

für Im(z) weiß ich im moment nicht weiter :-/