ich muss das Volumen von dieser Menge berechnen
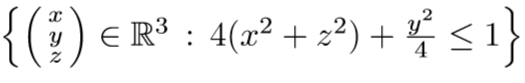
ich habe es am Anfang mit den normalen kartesischen Koordinaten berechnet
nämlich so :
\( \int\limits_{-2}^{2} \) \( \frac{π}{16} \) (4-y2)dy und kam auf \( \frac{2}{3} \)π
allerdings wollte ich die gleiche Rechnung mit Kugelkoordinaten machen, damit ich sehe ob ich das mit Kugelkoordinaten verstanden habe und habe mein Integral auf folgendes transformiert
\( \int\limits_{0}^{2π} \) \( \int\limits_{0}^{π} \) \( \int\limits_{0}^{1} \)1/2 r2cos(Θ)drdΘdα allerdings kommt bei diesem Integral 0 raus ! wegen sin(pi) und sin(0) ! könnte mir jemand sagen wo der Fehler liegt ? und was ich falsch gemacht habe ?
die 1/2 vor r2cos(Θ) ist a mal b mal c
Das wird mir wirklich sehr gut helfen !
Dankeschön