Unter diesem Titel führte das Land Hessen ein Projekt unter der wissenschaftlichen Leitung von Professorin Regina Bruder durch, für das im Februar 2005 eine Zusammenfassung der Ergebnisse vorgelegt wurde. Eine Beispielaufgabe dieses Projektes war sinngemäß folgende:
Riesenrad
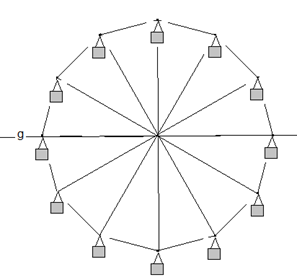
Ein Riesenrad hat den Durchmesser 60 m
a) Wie hoch über oder wie tief unter der Geraden g befinden sich die Aufhängepunkte der 12 Gondeln?
b) Betrachte die äußerste rechte Gondel. Beschreibe die Zuordnung Drehwinkel α der Gondel → Höhe des Aufhängepunktes der Gondel über (unter) der Geraden g durch eine Funktionsgleichung.
c) Welche Bedeutung könnten negative Drehwinkel im Sachzusammenhang haben?
Das ist zweifellos eine sehr hübsche Aufgabe. Unklar bleibt indessen, welchen Sinn der CAS-Einsatz bei der Bearbeitung dieser Aufgabe haben soll.
Die Definition des Sinus muss mit oder ohne CAS-Einsatz bekannt sein.
Zur Lösung von Aufgabe a) genügt ein Taschenrechner mit Sinusfunktion (wenn das halbe gleichseitige Dreieck erkannt wird, genügt sogar ein Taschenrechner mit Wurzelfunktion).
Die Lösungen der Aufgaben b) und c) erfordern keinen CAS-Einsatz und werden durch diesen auch nicht unterstützt.
Das Autorenteam schreibt zuvor:
„Hier finden sich Aufgaben [...], in denen trigonometrische Funktionen visualisiert werden. Ohne Rechnerunterstützung wäre das sicher nicht möglich, [...].“
Der zweite Satz ist schlicht nicht wahr. Auch in der vordigitalen Zeit haben Schüler Sinusfunktionen (händisch) visualisiert. Ist das nach Einführung digitaler Werkzeuge unmöglich geworden?
Alternativ soll folgende Aufgabe für einen sinnvollen CAS-Einsatz vorgeschlagen werden:
Regula falsi
a) Zeige: Mit je zwei gegebenen Punkten A(xa|ya) und B(xb|yb) lässt sich die Nullstelle xN der Geraden durch diese beiden Punkte in Abhängigkeit von den Koordinaten der gegebenen Punkte bestimmen als \( x_N = \frac{y_ax_b-y_bx_a}{y_a-y_b} \) .
b) Gegeben ist eine Funktion f mit der Gleichung f(x)=x3-3x+1. Diese hat eine Nullstelle xN zwischen x=1 und x=2. Zeige: Die Nullstelle xn der Geraden durch A(1|f(1)) und B(2|f(2)) liegt dichter an xN, als x=1 oder x=2.
c) Berechne die Nullstelle xn+1 der Geraden durch An(xn|f(xn)) und B(2|f(2)). Baue diesen Ansatz zu einem Näherungsverfahren aus und bestimme xN auf 5 Stellen hinter dem Komma genau.
Aufgabe a) könnte mit einigem Aufwand auch ohne CAS gelöst werden. Da sie aber nur als Vorbereitung auf weitergehende Gedanken gilt, ist der Termumformungs-Aufwand ohne CAS unangemessen.
Aufgabe b) kann mittels CAS gut visualisiert werden, während eine Visualisierung ohne CAS erheblichen Aufwand erfordert.
Aufgabe c) wird mit CAS leicht gelöst, wenn zunächst eine Rekursionsformel formuliert wurde.
Fazit:
Um von einem sinnvollen CAS-Einsatz sprechen zu können, muss vorab geklärt werden, was einen sinnvollen CAS-Einsatz auszeichnet. Der Sinn eines CAS-Einsatzes liegt im besonderen Maße in seinem Beitrag zur mathematischen Begriffsbildung. Dies wird auch in der didaktischen Literatur immer wieder betont.
Die CAS-Lösung der Aufgabe „Regula falsi“ trägt vor allem zur Festigung der Begriffes „Näherungsverfahren“ bei. Auch die fundamentale Idee des funktionalen Zusammenhangs kann mittels CAS untermauert werden. Im Beispiel „Riesenrad“ erhält der Zugang zum funktionalen Zusammenhang seinen wesentlichen Impuls vor allem durch die Einbettung in eine reale Anwendung und weniger bis gar nicht durch den Einsatz von CAS.
*CAS = Computer-Algebra-System. Dient zur Bearbeitung algebraischer Ausdrücke und löst auch symbolische Ausdrücke wie Variablen, Funktionen, Polynomen und Matrizen