Ich habe schon mal angefangen, muss aber weg. Ich mache später weiter.
f(x) = (2·SIN(x) - 1)/x
f'(x) = (2·x·COS(x) - 2·SIN(x) + 1)/x^2
a) Bestimmen Sie den Winkel, unter dem der Graph die x-Achse in den Punkten A bzw. B schneidet.
Nullstellen f(x) = 0
2·SIN(x) - 1 = 0
x = 5/6·pi ∨ x = pi/6
arctan(f'(1/6·pi)) = 73.18°
arctan(f'(5/6·pi)) = -33.49°
b) bestimmen Sie die Punkte C und D des Graphen von f mit waagerechter Tangente.
Steigung von Null f'(x) = 0
2·x·COS(x) - 2·SIN(x) + 1 = 0
Hier findet man die Nullstellen am einfachsten mit einem Näherungsverfahren.
x = 1.202
f(1.202) = 0.7201
x = 4.376
f(4.376) = -0.6599
c) Gibt es einen Punkt auf dem Graphen von f, mit dem die Steigung 1 ist?
Steigung von Null f'(x) = 1
(2·x·COS(x) - 2·SIN(x) + 1)/x^2 = 1
x = 0.8144
f(0.8144) = 0.5582
d) Haben die Schnittpunkte E und F der Graphen von f und f' eine besondere Bedeutung?
Dort ist der Funktionswert gleich der Steigung.
e) Bestimmen Sie anhand des Graphen die Wertemenge von f und f'. Was sind deren Bedeutung?
Ist aus dem Graphen abzulesen
f) Ermitteln Sie den Punkt, in dem die Steigung des Graphen von f den kleinsten Wert hat.
Ist das nicht der Punkt mit der waagerechten Tangente?
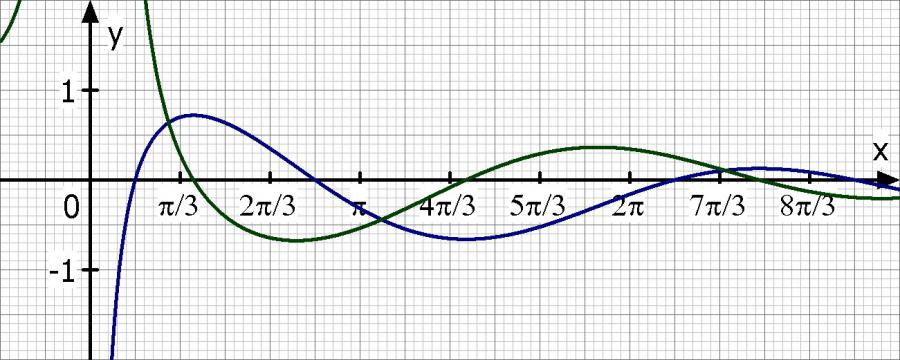
Skizze: