Kurvendiskussion umgekehrt

Question

eine polynomfunktion p zweiten Grades wird von der Geraden g:4y=8x-21 im Punkt P(3/yp) berührt. der Flächeninhalt unter der Funktion zwischen x=3 und x=5 beträgt 7 1/2 Flächeneinheiten.

a) Bestimme die Funktionsgleichung von p

b) Ermittle alle Nullstellen, Hoch und Tiefpunkte von p und die Gleichung der Tangente an p im Punkt Q(0/yq)

Answer 1

g: 4·y = 8·x - 21 oder y = 2·x - 5.25

f(x) = a·x^2 + b·x + c
f'(x) = 2·a·x + b
F(x) = 1/3·a·x^3 + 1/2·b·x^2 + c·x

f(3) = 0.75
9·a + 3·b + c = 0.75

f'(3) = 2
6·a + b = 2

F(5) - F(3) = 7.5
98/3·a + 8·b + 2·c = 7.5

Die Lösung des LGS lautet: a = 0.75 ∧ b = -2.5 ∧ c = 1.5

f(x) = 0.75·x^2 - 2.5·x + 1.5

Skizze:

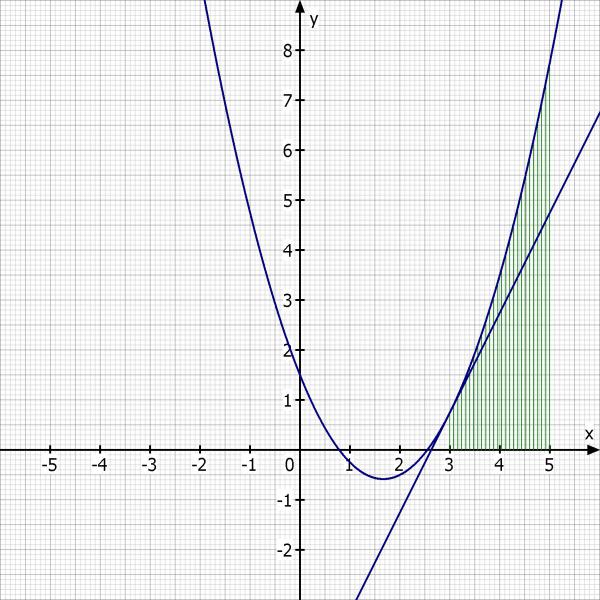
Die jetzige Kurvendiskussion solltest du wohl alleine hinbekommen oder?