Ich nehme auch einfach mal an, dass nicht ein kugelförmiger, sondern ein kegelförmiger Trichter gemeint ist, der zudem unten spitzt zuläuft, also keine Abflussröhre hat (ein solcher Körper wird in mathematischen Aufgabenstellungen häufig als Sektkelch bezeichnet).
Wenn ein solcher Kelch einen Öffnungswinkel von 60° hat, dann bilden seine Wände zusammen mit der Oberfläche der eingefüllten Masse im vertikalen Querschnitt ein gleichseitiges Dreieck. Dazu eine Skizze:
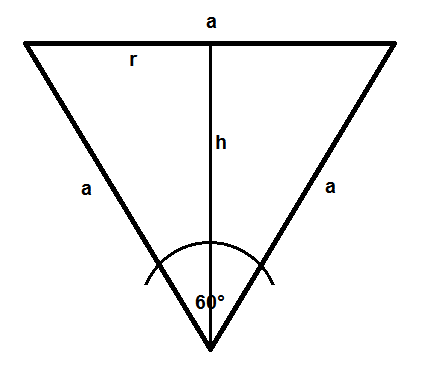
Nun gilt zum einen für das Volumen V eines Kegels:
V = g * h / 3
mit g: Grundflächeninhalt , h: Höhe
Die Grundfläche wird im vorliegenden Beispiel durch die Oberfläche der eingefüllten Masse gebildet. Für den kreisförmigen Grundflächeninhalt g gilt dabei:
g = pi * r ²
mit r: Radius der Grundfläche (also der Oberfläche der eingefüllten Masse).
Eingesetzt in die Volumenformel ergibt sich:
V = pi * r ² * h / 3
Zum anderen gilt in einem gleichseitigen Dreieck mit der Seitenlänge a und der Höhe h (Pythagoras):
( a / 2 ) ² + h ² = a ²
<=> h ² = ( 3 / 4 ) a ²
<=> h ² / 3 = a ² / 4 = ( a / 2 ) ²
Da die halbe Seitenlänge ( a / 2 ) gerade dem Radius r der Grundfläche des oben betrachteten Kegels entspricht, gilt also:
r ² = ( a / 2 ) ² = h ² / 3
In der oben fett gesetzten Formel kann daher r ² durch h ² / 3 ersetzt werden. Man erhält:
V = pi * ( h ² / 3 ) * h / 3 = pi * h ³ / 9
Auflösen nach h ergibt:
h = 3√ ( 9 * V / pi )
Setzt man hier nun das gegebene Volumen V = 1393,67 cm ³ ein, so erhält man:
h = 3√ ( 9 * 1393,67 / pi ) = 15,86 cm
Die eingefüllte Masse wird also in dem Kelch (Trichter) 15,86 cm hoch stehen.