Anfangswertproblem zum Abkühlungsgesetz und zu Ötzi herleiten

Question

Wie kann ich hier ein AWP herleiten? Kann mi bitte jemand helfen bei der Aufgabe.

a) Ein physikalisches Gesetz besagt: Die Abkühlgeschwindigkeit eines Körpers ist proportional zur Temperaturdifferenz zur Umgebung.

Ein Tasse Tee habe eine Anfangstemperatur von 80°C zum Zeitpunkt t_o = O. Durch die Umgebungstemperatur von 20°C kühlt der Tee ab, so dass er nach fünf Minuten nur noch 60°C heiß ist.

Leiten Sie ein AWP als mathematisches Modell für diesen Abkühlungsvorgang her. Lösen Sie das AWP und berechnen Sie, wie lange es dauert, bis sich der Körper auf 30°C abgekiihlt hat.

b) Am 19. September 1991 wurde in den Ötztaler Alpen eine Gletschermumie ("Ötzi") gefunden. Zur Ermittlung des genauen Todeszeitraums haben die Wissenschaftler die Radiokarbonmethode (oder: ¹⁴C-Methode) verwendet. Diese Methode beruht darauf, dass in abgestorbenen Organismen die Menge an gebundenen radioaktiven ¹⁴C-Atomen gemäß dem Zerfallsgesetz abnimmt. Lebende Organismen sind von diesem Effekt nicht betroffen, da sie ständig neuen Kohlenstoff aus der Umwelt aufnehmen, der wieder den normalen Anteil an ¹⁴C-Atomen einbringt.

Die Halbwertszeit des Kohlenstoffsotops ¹⁴C beträgt ca. 5730 Jahre.

Die Auswertung der Messergebnisse ergab, dass die Mumie zum Messzeitpunkt im Jahre 1991 etwa 52% bis 54% der ursprünglichen Menge 14C enthielt. Berechnen Sie mit Hilfe dieser Daten den Zeitraum, in dem Ötzi verstorben ist.

Liebe Grüße

Comments

Soll ich den ganzen Text aufschreiben?

---

Das ist für Dich doch nur ein Copy und Paste, also ja bitte ab"schreiben". Das hat für uns als Forum wie auch als Helfer viele Vorteile: Direktes Kopieren von eventuellen Werten, die Suchfunktion tut sich einfacher etc etc ;)

Answer 1

Hallo

 Abkühlgeschwindigkeit ist dT/dt = Änderung der Temperatur T pro Zeit

 also gilt dT/dt=k*(T-Te) Te=Umgebungs oder Endtemperatur.

lösen k aus T(5min)

b)C(t)=C(0)2^-t/5730,  t in Jahren  mit e Funktion 2=e^ln(2)

Gruß lul

Comments

Hallo lul, danke dir für deine Mühe,

also ich habe diese Gleichung ; k*(T-Te) Te=60° 

soll ich jetzt die Gleichung nach K auflösen un berechnen?

K=60/(T-Te)Te ?

---

Hallo

 ich hatte dir die Differentialgleichung aufgeschrieben, die musst du lösen: dT/(Te-T)=kdt integrieren, für die Integrationskonstante T(0) einsetzen für k T(5min) einsetzen. was du schreibst macht für mich keinen Sinn.

Gruß lul

---

Hallo lul,

tut mir leid ich hatte Sie nicht verstanden.

dT/dt=k*(T-Te) Te;  Sie haben daraus die dT/(Te-T)=kdt aufgestellt. Fehlt hier nicht Te unter dem Bruch

ich habe: dT/(Te-T)Te=kdt

Gruß

---

Hallo

 dass dT/dt nicht von Te^2 abhängen kann sollte dir klar sein, schon wegen der einheiten was sollten Grad^2 sein. in meinem post fehlte wohl ein Komma: dT/dt=k*(T-Te), Te=Umgebungs....

 also richtig dT/(Te-T)=kdt

Gruß lul

---

Hallo lul,

ich hoffe ich habe Sie richtig verstanden!

Habe ich die Dgl. richtig integriert?

Gruß

---

hallo

 mit u=Te-t  ist du  einfach -dT wo dein c herkommt verstehe ich nicht

 also hast du -lnu=t+c also ln(Te-T)=-kt +C

 oder Te-T=C1*e^-kt.  daraus T und T(0)=80°C also

-60°C=C*e^0

dein Zettel ist wirklich kaum lesbar, bessere Fotos oder echt schwarzer Stift würde helfen.

Gruß lul

---

Hallo lul,

hier nochmal die Berechnung

Gruß

---

hier neue Berechnung

---

Hallo

 es wäre viel freundlicher du würdest hier eintippen, dann kann ich zitieren,  ich hatte mal geschrieben te= Endtemperatur, ein bissen musst du doch auch mitdenken! du hast jetzt richtig

ln(T_e-T)=-k*t+C

 daraus mit Exponentialfunktion

T_e-T(t)=C*e^-kt  oder T(t)=Te-C*e^-kt

jetzt T(0) einsetzen: 80°=20°-C*1 also C=-60°

T(t)=20°+60°*e^-kt  jetzt T(5Min)=60° einsetzen  und daraus k bestimmen (k=0.081/Min)

Gruß lul

---

k= 0,081/min.

---

k= 0,081/min.

Würde man mit Einheit so notieren: k= 0,081min^(-1).

---

Hallo lul, danke sehr,

ich verstehe nicht manchmal was Sie meinen..... es tut mir leid aber ich versuch mein bestes wirklich....

Beste Grüße

---

Hallo

 deine Rechnungen sind jetzt ja richtig, Nur die Einheit bei k fehlte. du dividierst ja nicht durch 5 sondern durch 5min deshalb k=0,081*1/min oder 0,081min^-1 , Was ist noch nicht klar?

lul

---

jetzt zu Aufgabenteil b) :
ich habe diese Formel:  t=(ln(Vk/V)) ÷ -lambda

-\lambda= 1,21·10-4 1/a
Weche Werte muss ich für Vk und V einsetzen?

Gruß

---

Ist das nicht einfach

0.5^(t/5730) = 0.53 --> t = 5248 Jahre

Er lebte also vor ca. 5280 Jahren.

---

Hallo

 du sagst nicht was Vk, V sein soll? da es sich nicht um Volumen handelt, meinst du vielleicht die Menge M(t)=M(0)*e^{-1,2*10^-4a^-1*t} ?

dann ist M(t)/M(0)=54%=0,54. dazu solltest du eben nicht fertige Formeln benutzen, sonder wie ich das Zerfallsgesetz.

Gruß lul

---

'' deine Rechnungen sind jetzt ja richtig, Nur die Einheit bei k fehlte. du dividierst ja nicht durch 5 sondern durch 5min deshalb k=0,081*1/min oder 0,081min-1 , Was ist noch nicht klar? ''

Das hier habe ich alles verstanden, hatte nur vergessen ( *1/min ) zu schreiben... Ich meinte so allgemein, wenn ich Sie nicht verstehen sollte....

Gruß

---

ich habe einfach diese Formel Vk=V*e^+lambda*t nach t umgestelt

VK ist das Verhältnis von C-14 zu C12, also das Verhältnis der Kohlenstoffisotope im Knochen
V ist das Verhältnis von C-14 zu C12 in der Luft/Umgebung, also das Verhältnis der Kohlenstoffisotope in der Umgebung, als das Lebewesen noch gelebt hat (ist (fast) gleich dem Verhältnis von heute).

---

 0,5^t/5730=0,53

ln0,5^t/5730 =ln0,53

(t/5730)*ln0,5=ln0,53

t*ln0,5=ln(0,53)*5730

t=(ln(0,53)*5730) / ln(0,5)

t = 5248

ich weißes aber nicht wie  Der_Mathecoach auf 5280 kommt...?

---

Da steht doch auch t=5248 danach eben Tipfehler oder noch mit 52% gerechnet.

lul

---

Naja. Heute ist nicht 1991. Es sind also noch weitere 28 Jahre bis heute vergangen. Und dann wird das ganze natürlich gerundet angegeben :)

5248 + 28 = 5276 ≈ 5280

Ok. Vielleicht hätte ich nicht runden sollen damit es einfacher nachvollziehbar ist.

Answer 2

Nach dem Newtonschen Abkühlungsgesetz

( t | T )
( min | C° )
( 0 | 80 )
( 5 | 60 )
Jetzt nehmen wir einmal an die Umgebungstemperatur
sei 0 °. das heißt die Flüssigkeit würde von 60 ° auf 0 °
abkühlen.
( 0 | 60 )
( 5 | 40 )
Abkühlung als Exponentialfunktion
T ( t ) = T0 * f ^t
T ( 0 ) = 60
T ( 5 ) = 60 * f ^5 = 40
60 * f ^5 = 40
40 / 60 = t ^5
5 * ln(f) = ln(2/3)
ln(f) = ln(2/3) / 5 | e hoch
f = e ^ (ln(2/3) / 5)
f = 0.9221

T ( t ) = 60 * 0.9221 ^t
die 20 ° noch hinzuaddieren
T ( t ) = 60 * 0.9221 ^t + 20

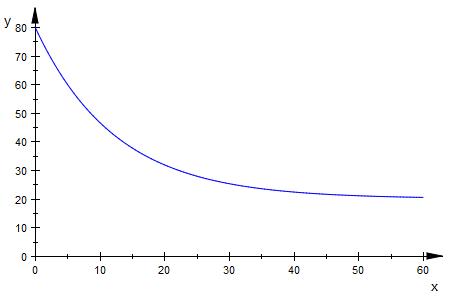
und berechnen Sie, wie lange es dauert, bis sich der Körper auf 30°C abgekiihlt hat.

60 * 0.9221 ^t + 20 = 30
t = 22.09 min

Comments

Vielen Dank ich habe alle Lösungen komplett verstanden....

Beste Grüße

---

Hallo Maike,
Zerfallsgesetz
Halbwertzeit : nach 5730 Jahren ist nur noch
die Hälfte der Anfangsmenge vorhanden
M ( t ) = aktuelle Menge
M0 = Anfangsmenge
M ( t ) = M0 * 1/2 ^(t/5730)
M ( t ) / M0 = 1/2 ^(t/5730)
M ( t ) / M0 = 53 % = 0.53
1/2 ^(t/5730) = 0.53 | ln
t/5730 * ln (0.5 ) = ln(0.53)
t = ln ( 0.53 ) / ln ( 0.5 ) * 5730
t = 5248 Jahre

Ich weiß nicht was ihr so kompliziert
rumrechnet.
Ob Zinsrechnung, Abkühlungsgesetz, Zerfalls-
gesetz : die Grundformel ist ( in Abwandlungen )
immer dieselbe. Eine Exponentialfunktion.
Da Übung den Meister macht stell ganz
einfach weitere Fragen zum Thema ein.
Oder zu dieser Antwort.

mfg Georg