Steigungswinkel und Geraden

Question

Wie geht das ??


Die Gerade h schneidet die x-Achse in x=3 und verläuft durch den Punkt  P(4/-1).

Bestimmen sie die Geradengleichung und den Steigungswinkel.

Answer 1

 

Geradengleichung allgemein

y = mx + b

oder

f(x) = f'(x₀) * (x - x₀) + f(x₀)

Wir haben die beiden Punkte P(4|-1) und Q (3|0)

Als x₀ nehmen wir die Stelle weiter rechts, also x₀ = 4

Dann haben wir schon

f(x) = f'(4) * (x - 4) + (-1)

Wir brauchen noch den Anstieg in x₀ = 4 und berechnen den mit Hilfe des Differenzenquotienten (y-Differenz / x-Differenz):

(4-3)/(-1-0) = 1/(-1) = -1

Also lautet die Geradengleichung:

f(x) = y = -1 * (x - 4) - 1 oder vereinfacht

f(x) = y = -x + 3

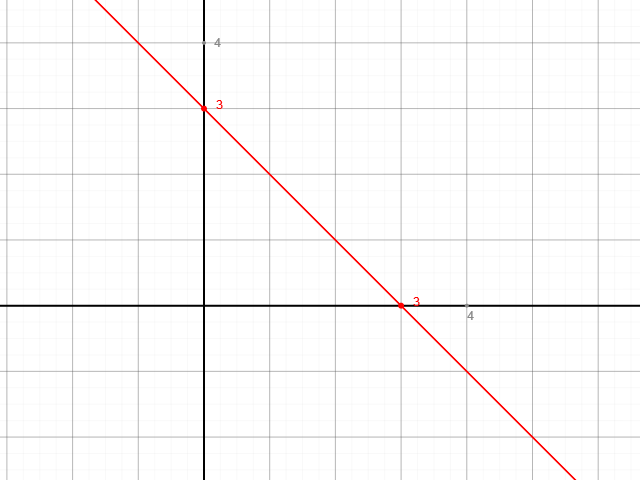
Den Steigungswinkel kann man direkt ablesen: -45°

 

Besten Gruß

Comments

Muss dann nicht 45° sein?? und nicht -45°??


Danke ;)

---

Gern geschehen :-)


45° wären es, wenn die Gerade schräg nach oben gehen würde, also z.B. vom Punkt (0|0) über (1|1) nach (2|2) usw.
Diese Gerade läuft aber schräg nach unten, deshalb kehrt sich das Vorzeichen um, also -45°.