Geradengleichung allgemein: f(x) = y = mx + b
m erhalten wir durch Berechnung der "y-Differenz" / "x-Differenz"
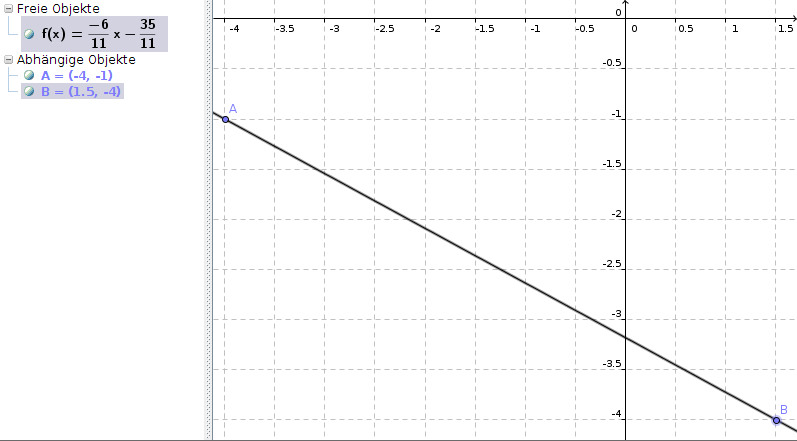
a) A (-4 | -1) B (1,5 | -4)
m = [-4 - (-1)] / [1,5 - (-4)] = -3/5,5 = -6/11
b erhalten wir, indem wir dieses m und einen Punkt (zum Beispiel B) in die allgemeine Geradengleichung einsetzen:
-4 = -6/11 * 1,5 + b
b = -4 + 6/11 * 1,5 = -35/11
Damit lautet die Geradengleichung
y = -6/11 * x - 35/11
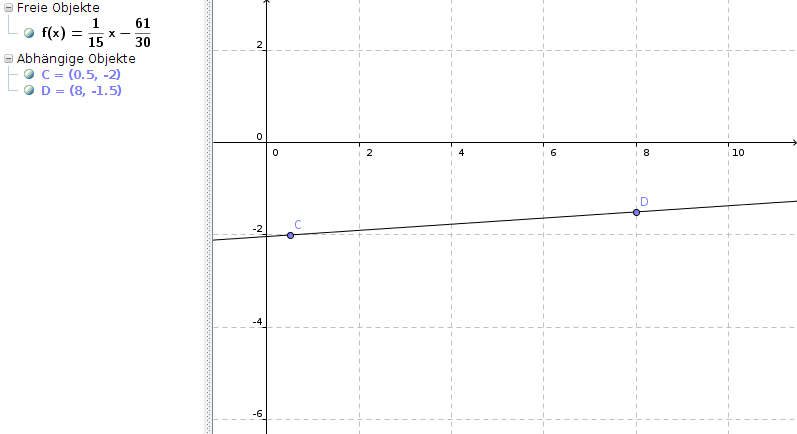
b) C (0,5 | -2) D (8 | -1,5)
Gleiches Vorgehen:
m = [-1,5 - (-2)] / (8 - 0,5) = 0,5/7,5 = 1/15
-1,5 = 1/15 * 8 + b
b = -1,5 - 1/15 * 8 = -22,5/15 - 8/15 = -30,5/15 = -61/30
f(x) = y = 1/15 * x - 61/30
Steigungswinkel zur y-Achse:
1. Ableitung der Geradengleichung bilden und y = 0 setzen, davon arctan {tan-1} nehmen
f'(x) = 1/15
f'(0) = 1/15
arctan(1/15) ≈ 3,81°
Besten Gruß