Hallo liebe Mathe-Fans,
ich habe eine Frage an alle Logarithmus Spezialisten. Ich habe folgende Gleichung gegeben:
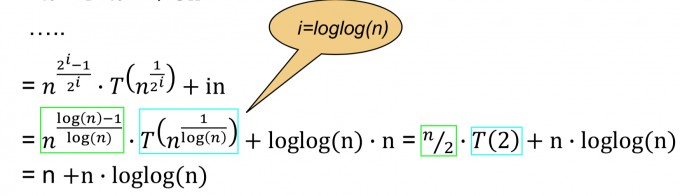
Mein Problem bezieht sich auf die von mir grün umrandete Umformung (eventuell auch um die blau umrandete).
Mein Ansatz ist der folgende:
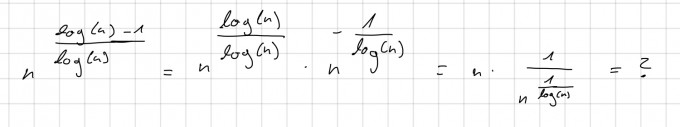
Ich hoffe, der Ansatz ist richtig. Wie komme ich auf die 1/2?
Das n habe ich ja schon, aber wie komme ich dann auf die 1/2? Unser Prof meinte, rechnet zuhause nach, und ich komme nicht drauf ^^
Und falls jemand die Lösung weiß könnte er mir sicher auch schon helfen, wie ich aus der blauen Umformung auf 2 komme ...
Ich hoffe jemand kann mir helfen. Liebe Grüße