Vom Duplikat:
Titel: Integral: Runde Brosche aus Gold Teil 2
Stichworte: integral
Aufgabe:
Ein Goldschmied möchte für seine Schmuckkollektion eine neue kreisförmige Brosche entwickeln.
a)
Die Form der Trennlinie zwischen den beiden Teilen der
Brosche entspricht der in der Abbildung 1 dargestellten
Funktion f(x). Die Achseneinheiten entsprechen jeweils 1 cm.
Bestimmen Sie die Funktion 3. Grades f(x), die den Verlauf der
in der Graphik dargestellten Trennlinie beschreibt.
Dokumentieren Sie auch Ihren Ansatz und Lösungsweg!
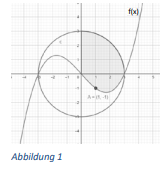
a)
f(x)=0,125x4 - 1,125x² (Ergebnis durch LGS)
c)
Bei einer zweiten Variante der Brosche wird zusätzlich zu der
durch f beschriebenen Trennlinie eine zweite Linie angebracht,
die durch die Funktion () = ∙ (), ≥ 1 beschrieben wird.
Bestimmen Sie den Faktor a so, dass der Flächeninhalt der in
Abbildung 2 markierten Fläche zwischen den beiden Trennlinien
1,62 cm² beträgt.
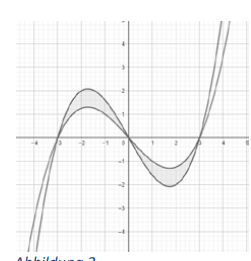
c)
Versuch zu 99,99% falsch (Angaben ohne Gewähr)
1,62 = \( \int\limits_{0}^{3} \) a∙ (0,125x4 - 1,125x²)
Ich bin hier unsicher, muss ich hier überhaupt die Fläche/Integral bestimmen
1,62 = a∙ (0,125x4 - 1,125x²)
d)
Der Abbau von Gold steht wegen der damit verbundenen Umweltbelastung zunehmend in
der Kritik. Der Goldschmied erhöht daher die Nutzung von Altgold für seine
Schmuckproduktion. Als er den Betrieb vor 10 Jahren übernommen hat, wurden pro Jahr
300 g Reingold aus Minenproduktion verbraucht. Seither wurde dieser Wert stetig um 10 %
jährlich gesenkt. Wie viel Gold aus Minenproduktion wird aktuell für die Produktion in der
Goldschmiede verbraucht? Wie viel Gold aus Minenproduktion wird die Goldschmiede
insgesamt benötigen, wenn der Betrieb ewig weiter betrieben wird und die Reduktion des
Verbrauches in gleicher Weise weitergeführt wird?
Das ist doch Geometrische Folge und n---> ∞?
a) an= a1*qn-1 =300*0,99 = 116,23
b) 1/1-q = 1/1-0,9=10
Was hab ich falsch gemacht?
!!