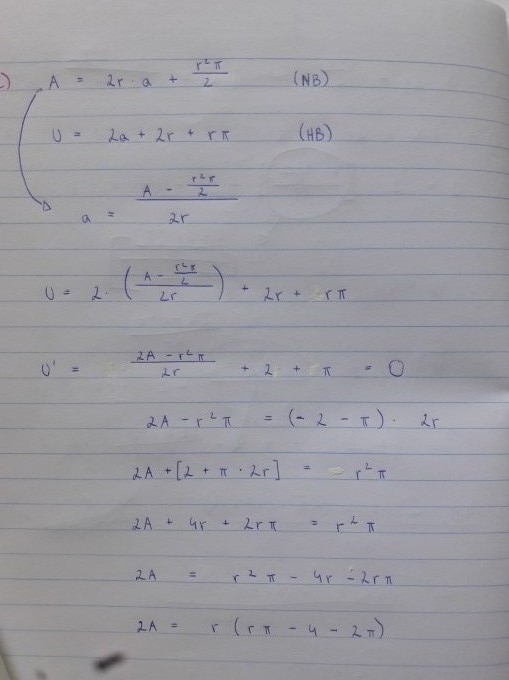Aufgabe:
Der Querschnitt eines Kanals soll die Form eines Rechtecks mit aufgesetztem Halbkreis erhalten und den Flächeninhalt A haben. Welche Maße muss der Kanal haben, damit zur Herstellung möglichst wenig Material benötigt wird (d.h. der Umfang des Querschnitts minimal wird) ?
Problem/Ansatz:
Kann mir jemand weiterhelfen? Oder erklären wieso mein Rechenweg falsch ist? (Ich hoffe meine Schrift ist gut leserlich)