Finde ein Minimales Erzeugendensystem S' enthalten in S von <S>

Question

Aufgabe:

Sei \(\mathbb{K} = \mathbb{Q}.\) Oder Sei \(\mathbb{K} = \mathbb{F}_2.\)
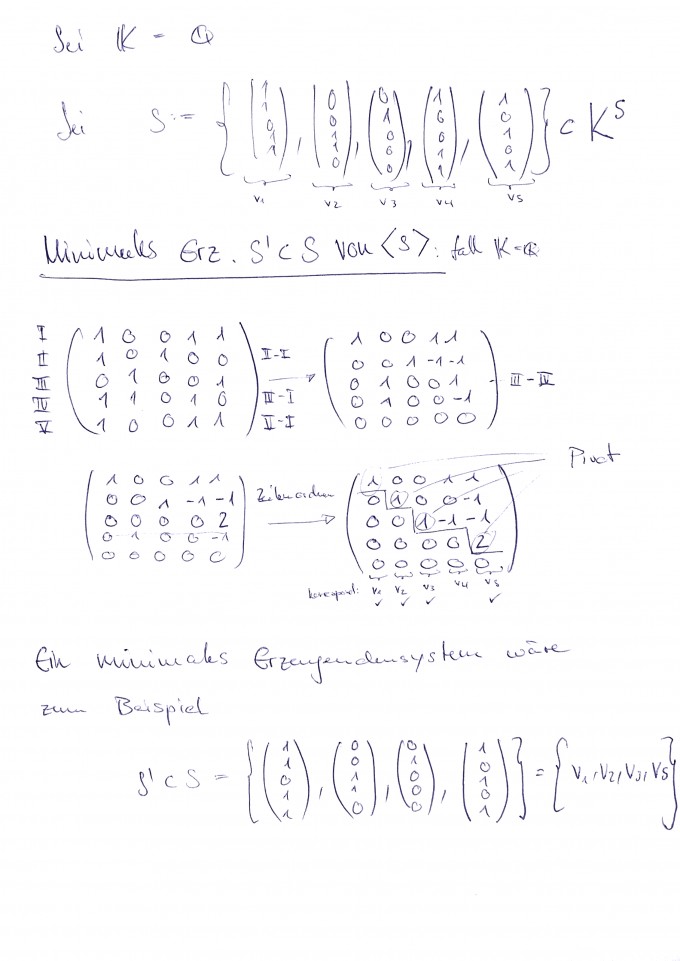
Finde ein Minimales Erzeugendensystem \(S'\) \(\subset\) \(S\) von \(⟨S⟩\).$$S :=\left\{\left(\begin{array}{l}{1} \\ {1} \\ {0} \\ {1} \\ {1}\end{array}\right),\left(\begin{array}{l}{0} \\ {0} \\ {1} \\ {1} \\ {0}\end{array}\right),\left(\begin{array}{l}{0} \\ {1} \\ {0} \\ {0} \\ {0}\end{array}\right),\left(\begin{array}{l}{1} \\ {0} \\ {0} \\ {1} \\ {1}\end{array}\right),\left(\begin{array}{l}{1} \\ {0} \\ {1} \\ {0} \\ {1}\end{array}\right)\right\} \subset K^{5}$$

Vorgehen: Fall \(\mathbb{K} = \mathbb{Q}.\)

(Ich schildere kurz bevor ich  unten mein Lösungsweg anfüge.)

Ich packe alle Spaltenvektoren in eine Matrix und eliminiere mit dem Gaussverfahren die linear abhängigen. 
Dann erhalte ich 4 Vektoren aus dem \(K^5\). 

Problem/Ansatz:
Das Problem ist, dass ich mit vier Vektoren vier Achsen habe, nehmen wir an es wären \(e_1, e_2, e_3, e_4,\) dann wären das die Basen von einem 4-dimensionalen Raum. 

Was verwirrt mich? 
Mich verwirrt, dass die einzelnen Vektoren aus dem \(K^5\) kommen.
Sie haben ja fünf Komponenten, da aber das, was die Vektoren aufspannen ein 4-dimensionaler Raum ist,
verwirrt mich das.
Denn ich erwarte intuitiv, dass der vierdimensionale Raum 4 linear Unabhängige Vektoren hat, und diese vier lin. unabhängigen Vektoren sollen jeweils vier Komponenten haben, denn jede Komponente erzeugt eine Dimension. 
Ich bekomme aber für \(S'\) vier Vektoren die jeweils fünf Komponenten haben. 

Frage:
Kann jemand etwas zu meiner Verwirrung sagen  ?




Mein Lösungsweg für K = Q:

Answer 1

Du hast fünf achsen,

Mich verwirrt, dass die einzelnen Vektoren aus dem K⁵ kommen.

Du hast 5 Achsen, aber eine davon verwendest du nicht.

denn jede Komponente erzeugt eine Dimension.

Wie sieht das dann mit der Ebene \(\left\{\vec{x}\in \mathbb{R}^3 | \exists r,s\in \mathbb{r} : \vec{x} = r\cdot  \begin{pmatrix} 1\\1\\1 \end{pmatrix}  + s\cdot  \begin{pmatrix} -1\\1\\0 \end{pmatrix}\right\} \) aus? Die ist ein zweidimensionaler Vektorraum, obwohl die Vektoren drei Komponenten haben.

Comments

Du hast 5 Achsen, aber eine davon verwendest du nicht.

Moment, 
ich muss überlegen. 

Ja, am Anfang besteht \(S\) aus fünf Vektoren zu jeweils 5 Komponente, das bedeutet, dass ein einziger Vektor, von jeder der fünf Achsen gebrauch machen muss um dargestellt zu werden.  

Aber S ist linear abhängig. 

Dann komme ich per Gauss auf S'. 
Dort habe ich nur 4 Vektoren a fünf Komponenten, also habe ich mit vier Vektoren a fünf Komponenten fünf Achsen oder vier Achsen ? 

Ich denke:
Ein vektor v = \( \begin{pmatrix} v_1\\v_2\\v_3\\v_4\\v_5 \end{pmatrix} \)
hat fünf achsen weil jede Komponente \(v_i\) für eine Achse steht. Oder?

Aber dann:
Habe ich in \(S'\) vier Vektoren a fünf Achsen. 

Frage1:
Und was das genau bedeutet weiss ich nicht ? 

Wie sieht es mit... ...Die ist ein zweidimensionaler Vektorraum, obwohl die Vektoren drei Komponenten haben.

Ja. Das sehe ich nicht auf den ersten Blick. Erst wenn ich per Gauss diese zwei Vektoren prüfe, sehe ich dass sie lin. unabhängig sind. 


Frage2:
Heisst dass, dass meine Vektoren, also wenn ich S' linearkombiniere einen vierdimensionalen Unterraum von ⟨S⟩ erhalte?

---

Heisst dass, dass meine Vektoren, also wenn ich S' linearkombiniere einen vierdimensionalen Unterraum von ⟨S⟩ erhalte?

Es bedeutet, dass ⟨S'⟩ = ⟨S⟩ ist. Das war ja auch so in der Aufgabenstellung gefordert.

Außerdem ist ⟨S'⟩ ein vierdimensionaler Unterraum von ℚ⁵.

---

Stimmt, an ⟨S'⟩ = ⟨S⟩ habe ich nicht gedacht. 

und das ⟨S'⟩ ein vierdimensionaler Unterraum von ℚ5 ist macht jetzt auch sinn.