Der zweite Strahlensatz: Försterdreiecks um Baumhöhe zu bestimmen?

Question

Aufgabe:

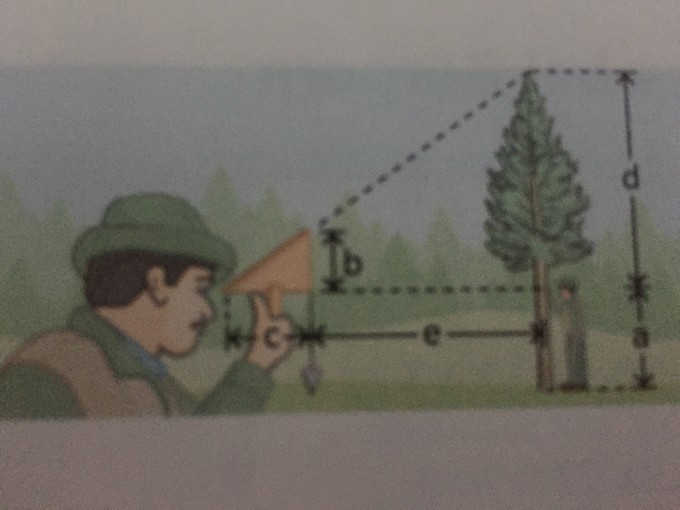
Die Abbildung zeigt einen Förster mit einem Försterdreieck.

a) Beschreibe, wie man mithilfe eines Försterdreiecks die Baumhöhe bestimmen kann

b) Bestimme die Baumhöhe für a = 1,6 cm,

b = 2 cm, c = 24 cm und e = 20 m.

Problem/Ansatz:

Könnte jemand mir zuzüglich A) ausführlich erklären..Danke

Answer 1

a)

d/(c + e) = b/c --> d = b·(e/c + 1)

Baumhöhe

h = a + d = a + b·(e/c + 1)

b) Bestimme die Baumhöhe für a = 1,6 cm, b = 2 cm, c = 24 cm und e = 20 m.

Prüfe hier bitte zunächst mal die Werte und die Einheiten !!

Comments

Hallo
Vielen Dank für Ihre schnelle Antwort.
Könnten Sie mir bitte den Aufgabenteil a)  ausführlich mit Sätzen erklären.

Vielen Dank
Kreuz

---

a) Beschreibe, wie man mithilfe eines Försterdreiecks die Baumhöhe bestimmen kann

Man stellt den Strahlensatz auf um aus b, c und e die Länge d zu ermitteln. Zur länge d wird im nachhinein noch a addiert um die Baumhöhe zu erhalten.

Answer 2

20m = 2000 cm

2/24=x/2024

x= 4048/24

Höhe des Baumes x+160

Comments

Hallo

Vielen Dank für Ihre schnelle Antwort.

Könnten Sie mir bitte den Aufgabenteil a)  ausführlich mit Sätzen erklären.

Vielen Dank

Kreuz

---

Das Försterdreieck ist rechtwinklig. Man häl es so, dass eine Kathete (c) in Augenhöhe (a) parallel zur Waagerechten (Erdboden) ist. Die Entferunng zum Baum e schreitet der Förster ab, wobei er seine Schrittlänge kennt. Dann richtet der Förster die Hypotenuse des Försterdreiecks auf die Baumspitze. Da er die Länge der senkrechten Kathete (b) kennt, gilt jetzt nach dem zweiten Strahlensatz b/c=d/(e+c) mit der Baumhöhe d+a