Gewinnfunktion mit mehreren Variablen (Differentialrechnung)

Question

es gibt wohl nichts besseres als sich bei diesem herrlichen Wetter auf die Wirtschaftsmathe Prüfung vorzubereiten.

Leider komme ich hier nicht weiter, eventuell kann mir da jemand helfen.

Wünsche einen schönen sonnigen Tag!

Lieben Gruß

Aufgabe 1
Ein Unternehmen stellt Pfannen (xP) und Töpfe (xT) her und möchte die Produktion
so gestalten, dass sein erwirtschafteter Gewinn maximal wird.
Seine Produktionskosten stellen sich folgendermaßen dar:

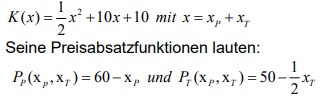
a) Stellen Sie die Gewinnfunktion auf.
b) Ermitteln Sie die gewinnmaximalen Mengen sowie den dabei erzielten Gewinn.

Und das wäre die 2. Aufgabe:

Answer 1

x = x_P

y = x_T

a)

G(x, y) = x·(60 - x) + y·(50 - 0.5·y) - (0.5·(x + y)^2 + 10·(x + y) + 10)

G(x, y) = - 1.5·x^2 - x·y + 50·x - y^2 + 40·y - 10

b)

G'(x, y) = [- 3·x - y + 50, -x - 2·y + 40] = [0, 0] --> x = 12 ∧ y = 14

G(12, 14) = 570

Comments

Wow,

super lieben Dank für die schnelle Antwort!
Könntest du mir bei Aufgabe 2) ebenfalls helfen?

Lieben Gruß

---

Da die zweite Aufgabe nichts mit der ersten zu tun hat solltest du sie getrennt einstellen.

Da aber die zweite Aufgabe ähnlich wie die erste gerechnet wird könntest du dich auch zuerst selber an der anderen probieren.

Tipp

G(x, y) = x·(1280 - 4·x + y) + y·(2360 + 2·x - 3·y) - (0.5·x^2 + x·y + y^2 + 500000)

G(x, y) = - 9/2·x^2 + 2·x·y + 1280·x - 4·y^2 + 2360·y - 500000