a und b so bestimmen, dass die Funktion differenzierbar ist

Question

Aufgabe:

Nachtrag: in der 2.Zeile steht bx-e für x>1

 wie bestimme ich hier a und b so, dass die Funktion differenzierbar ist ?
Problem/Ansatz:

Comments

wie soll das in der 2.Zeile heißen

bx minus ???

---

Genau es soll heißen  : bx-e

Answer 1

f ( x ) = e^(a*x) 
g ( x ) = b * x - e

f ´( x ) = e^(a*x) * a
g ´( x ) = b

Stetigkeit
f = g
e^(a*x)  = b * x - e

Differenzierbarkeit
f ´= g
e^(a*x) * a = b

an der Stelle x = 1
e^(a*1)  = b * 1 - e
e^(a)  = b  - e

e^(a*x) * a = b
e^(a) * a = b

e^(a)  = b  - e
b = e^a + e

e^(a) * a = b
e^(a) * a = e^a + e
Newton
a = 1.567

b = e^(1.567) + e
b = 7.511

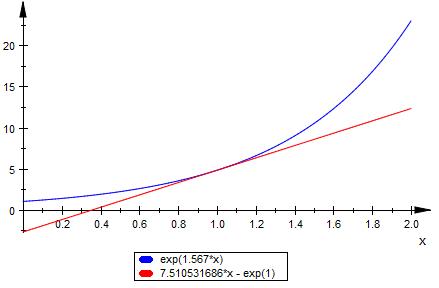
f ( x ) = e^(1.567*x)
g ( x ) = 7.511 * x - e

 

Answer 2

f(x)=\( \begin{pmatrix} e^x für x≤1\\ex für x>1 \end{pmatrix} \)

Comments

Mhmm meine funktion lautet anders

---

f(x) = e^ax für x <=1 und

          bx-e für x grösser 1

---

Roland vermutet als Resultat a = 1 und b = ?, wenn bx - e = ex ?

Was soll das überhaupt heissen?

wie bestimme ich hier a und b so, dass die Funktion differenzierbar ist ?

Vielleicht so:

wie bestimme ich hier a und b so, dass die Funktion im ganzen Definitionsbereich ℝ differenzierbar ist ?

?