Ich habe auch den Rest der Aufgabe mal unter https://docs.google.com/document/d/1bZBQqC84mmT6iEPi3nTMh32JNxJ2mabPpPDSXBmwV8o/pub bereitgestellt. Wie lautet die Aufgabe e) ?
Lösungen:
a) Wie lautet die Definitionsmenge von f?
Der ln(z) ist nur Definiert für z > 0
x^2 > 0
x ≠ 0
b) Begründen Sie, weshalb x = 0 keine Nullstelle von f ist, obwohl für x = 0 ein Faktor des Funktionsterms null wird.
Weil x = 0 nicht im Definitionsbereich der Funktion liegt.
c) Bestimmen Sie die Nullstellen von f.
Nullstellen f(x) = 0
x·(LN(x^2) - 2) = 0
LN(x^2) - 2 = 0
LN(x^2) = 2
x^2 = e^2
x = ± e
d) Untersuchen Sie f auf Extrem- und Wendepunkte.
Extrempunkte f'(x) = 0
LN(x^2) = 0
x^2 = e^0 = 1
x = ± 1
f(-1) = 2 --> Hochpunkt
f(1) = -2 --> Tiefpunkt
Wendepunkte f''(x) = 0
2/x = 0
2 ≠ 0
Es gibt keine Wendepunkte.
f) Wo schneidet die Gerade g(x) = - 2·x den Graphen von f?
f(x) = g(x)
x·(LN(x^2) - 2) = - 2·x
LN(x^2) - 2 = - 2
LN(x^2) = 0
x^2 = e^0 = 1
x = ± 1
Y- Koordinaten siehe oben.
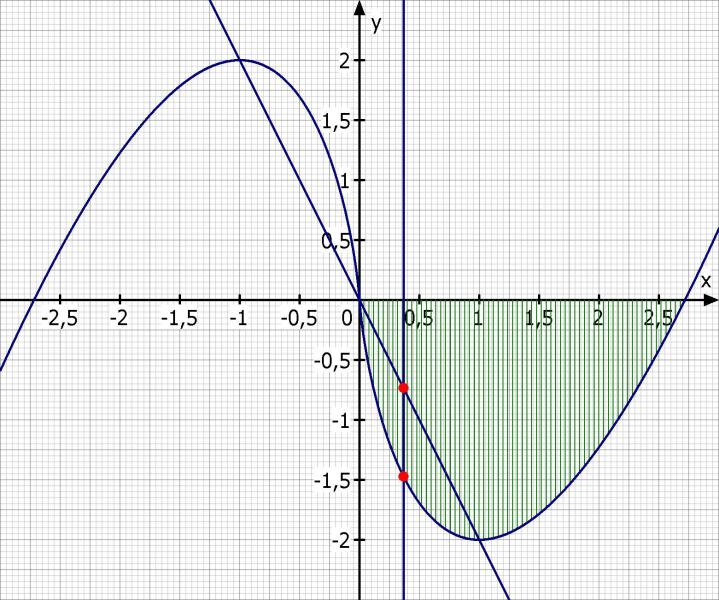
g) Die vertikale Gerade x = z mit 0 < z ≤ 1 schneidet den Graphen von f im Punkt A und den Graphen von g im Punkt B. Wie muss z gewählt werden, damit die Länge der Strecke AB möglichst groß wird?
Maximieren:
d(x) = f(x) - g(x) = x·(LN(x^2) - 2) - (- 2·x) = x·LN(x^2)
d'(x) = LN(x^2) + 2 = 0
LN(x^2) = -2
x^2 = e^{-2} = 1/e^2
x = ± 1/e
h) Bestimmen Sie eine Stammfunktion von f.
∫ x·(LN(x^2) - 2) dx
Substitution z = x^2 und dz = 2·x dx
∫ x·(LN(z) - 2) dz/(2·x)
∫ 1/2·(LN(z) - 2) dz
∫ (1/2·LN(z) - 1) dz
1/2·z·(LN(z) - 1) - z
1/2·z·LN(z) - 1/2·z - z
1/2·z·LN(z) - 3/2·z
Resubstitution
1/2·x^2·LN(x^2) - 3/2·x^2
i) Der Graph von f schließt mit den Koordinatenachsen im 4. Quadranten ein Flächenstück ein. Berechnen Sie dessen Inhalt.
F(e) - F(0) = 1/2·e^2·LN(e^2) - 3/2·e^2 - (1/2·0^2·LN(0^2) - 3/2·0^2) = -1/2·e^2
Achtung: Obige Gleichung ist so nicht korrekt weil der ln(0) nicht definiert ist. Hier muss man also den Grenzwert für x → 0 berechnen.
