Anzahl der Nullstellen bestimmen f(x) = 20x^{6} + 52x^{5} -15x^{4} - 80x^{3} - 40x^{2} + 6. Wozu ableiten?

Question

Aufgabe:

Hallo. Kann mir jemand erklären, wie ich zu der Anzahl der Nullstellen von Funktionen im Allgemeinen komme?

ich habe hier ein paar Beispiele:

$$e^\frac{x}{5}=2x-5$$

$$f(x) = 20x^{6} + 52x^{5} -15x^{4} - 80x^{3} - 40x^{2} + {6}$$

Was bringt mir die Anwendung der Ableitung, bei der Lösung dieser Frage?

Vielen Dank der Community

Dan

Comments

Die Anzahl der Nullstellen eines reellen Polynoms in einem gegebeben Intervall lässt sich auch mit dem Verfahren der Sturmschen Kette ermitteln.

---

a)

$$e^\frac{x}{5}=2x-5$$

Hier solltest du nicht von der Anzahl der Nullstellen sondern von der Anzahl der Lösungen dieser Gleichung sprechen.

b) passt zu deiner Fragestellung.

Answer 1

Was bring mir die Anwendung der Ableitung, bei der Lösung dieser Frage?

Wenn ein Extrempunkt über Null und der nächste unter Null liegt muss es dazwischen eine Nullstelle geben. Zumindest wenn sie im gesamten Intervall definiert und stetig ist.

Könntest du die Graphen der Terme auf beiden Seiten der Gleichung skizzieren? Könntest du auch den Graphen des Polynoms skizzieren?

Skizze 1:

~plot~ e^(x/5);2x-5;[[-1|20|-1|30]] ~plot~

Skizze 2:

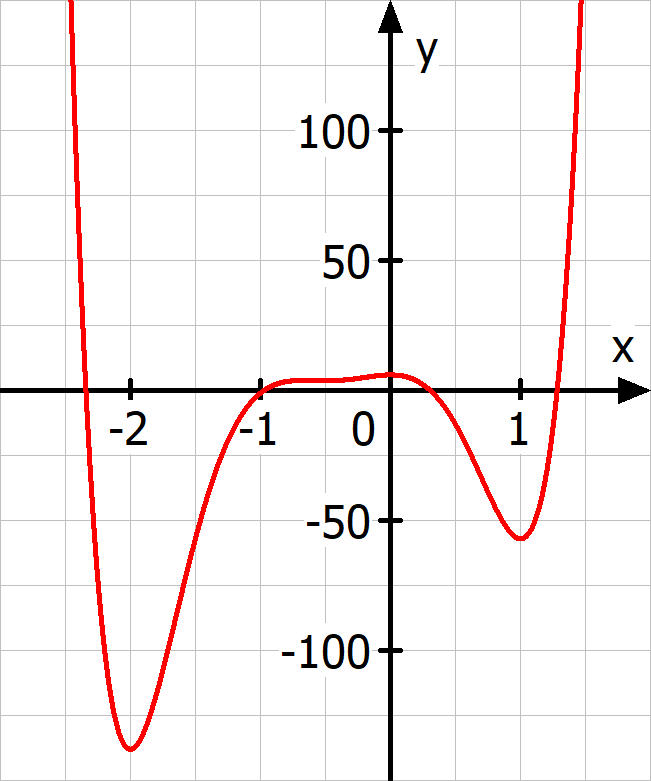
f(x) = 20·x^6 + 52·x^5 - 15·x^4 - 80·x^3 - 40·x^2 + 6

f'(x) = 120·x^5 + 260·x^4 - 60·x^3 - 240·x^2 - 80·x = 0 --> x = - 2/3 ∨ x = - 1/2 ∨ x = -2 ∨ x = 1 ∨ x = 0

lim (x --> -∞) f(x) = ∞
irgendwo eine Nullstelle
f(-2) = -138
irgendwo eine Nullstelle
f(- 2/3) = 2822/729
f(- 1/2) = 15/4
f(0) = 6
irgendwo eine Nullstelle
f(1) = -57
irgendwo eine Nullstelle
lim (x → ∞) f(x) = ∞

Ich zähle 4 Nullstellen.

Answer 2

e^x/5=2x−5. In diesem Falle kenne ich keine allgemeine, einfache Regel
f(x)=20x⁶+52x⁵−15x⁴−80x³−40x²+6. Die höchste Potenz (6) nennt die maximale Anzahl der reellen Nullstellen.

An einer einfachen (ungeraden) Nullstelle ist die Ableitung ≠0.

An einer doppelten (geraden) Nullstelle ist die Ableitung =0.

Comments

ex/5=2x−5. In diesem Falle kenne ich keine allgemeine, einfache Regel

Auch dort gilt, was ich oben gesagt hatte. Man untersucht

y = e^(x/5) - (2·x - 5)

auf Extrempunkte

y' = e^(x/5)/5 - 2 = 0 --> x = 5·LN(10) = 11.51

y(11.51) = -8.026

Da die Grenzwerte von y = e^(x/5) - (2·x - 5) für x gegen ±∞ bei +∞ liegen hat man genau 2 Nullstellen.

Wählt man jetzt z.B. das Newtonverfahren kann man als Startwerte z.B. 11 und 12 benutzen um die beiden Nullstellen zu erhalten.

---

Ist das eine "einfache Regel"?

---

Ist das eine "einfache Regel"?

Ja. Hoch und Tiefpunkte auf Vorzeichenwechsel zu untersuchen ist doch sehr einfach.

Man muss aber gestehen das man das im Rahmen der Schulmathematik eigentlich nie benötigt. Ich glaube ich habe das Verfahren überhaupt erst zweimal verwendet.

Liegt aber auch daran, dass wenn man einen Rechner hat der den Graphen skizziert man schon näherungsweise die Nullstellen ablesen kann ohne zu rechnen. Das ist dann natürlich noch wesentlich einfacher :)