a/a‘=sin(alfa)/sin(delta+alfa) Was ist alfa?

Question

Aufgabe:

Ich habe zwei Straffen von Blech mit unterschiedliche Breite.

a=210

a'=331

delta=32°

Was ist alfa?

a/a‘=sin(alfa)/sin(delta+alfa)

Ich kenne daß im dieses Beispiel: Alfa=36° ist, aber das universales Formel kenne ich nicht. Wie soll ich fortsetzen?

Danke schon!

Xerostomus

Comments

https://de.wikipedia.org/wiki/Alpha entspricht der deutschen Rechtschreibung. 

Z.B. auf Italienisch, Finnisch, Estnisch und Schwedisch schreibt man dagegen alfa.

---

Mathecouche is ein kluger Kerl!!!

α = ARCTAN(a·SIN(δ)/(a' - a·COS(δ)))

I habe für mich endlich eine andere Lösung gefunden:

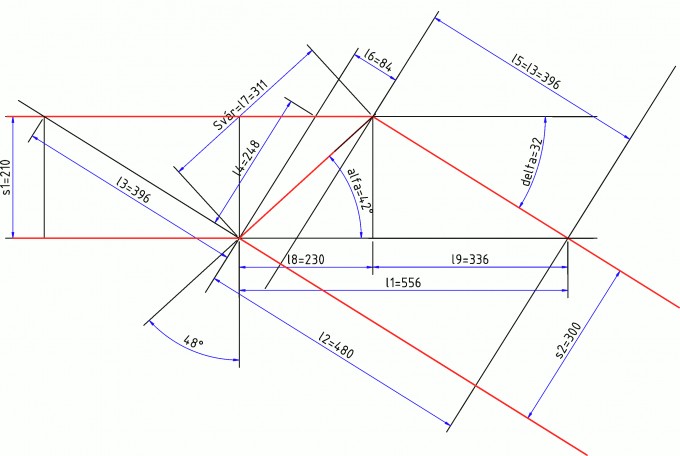
Wir starten mit [S1, S2, delta] und dann wir können lösen: l1, l2... bis l9. Und es ist nur sin() und Pythagoras. Einfacher, aber die Gleichung der Mathecouch ist mehr elegant.

Aber ich steht noch nicht verstehe, wie man zum Lösung von Mathecouche kommen kann...

Answer 1

Die universelle Gleichung hattest du doch bereits notiert

a/a' = SIN(α)/SIN(α + δ)
oder
a·SIN(α + δ) - a'·SIN(α) = 0

Ich denke zur Not kann man das jetzt mit einem Näherungsverfahren lösen oder brauchst du die Lösung exakt?

Dann kann ich dich trösten 36° ist eben nicht die exakte Lösung sondern auch nur eine Näherung.

Comments

Die Gleichung lässt sich auch elementar nach α auflösen.

---

Die Gleichung lässt sich auch elemantar nach α auflösen.

Dann darfst du das gerne als Antwort beisteuern, wenn du dir die Mühe machen möchtest.

---

Hallo

Speck hat natürlich rech, man muss nur durch cos dividieren, mein Ansatz war also dumm bzw. zu umständlich. Wir wissen aber immer noch nicht, was das genaue Problem ist, da man Strafen ja sehr verschieden aneinander legen kann.

lul

---

Elementar aufgelöst:

α = ARCTAN(a·SIN(δ)/(a' - a·COS(δ)))

Ist allerdings die Frage ob das nötig ist.

---

Diese Frage hast du bereits selbst beantwortet als du schriebst

... zur Not kann man das jetzt mit einem Näherungsverfahren lösen...

Answer 2

Der grün eingezeichnete 180°-Winkel besteht aus den 4 Teilwinkeln α, β', 90° und δ.

Damit gilt  β'+( α+δ)=90°.

Die in beiden Streifen vorkommende gemeinsame Länge c ist einerseits

c=a / sin α, andererseits c=a'/ cos  β'.

Wegen  β'+( α+δ)=90° gilt   cos  β'=sin(α+δ)

Aus der Gleichheit a / sin α =a'/ cos  β' folgt somit

a / sin α =a'/ sin(α+δ) 

Answer 3

Hallo

 eigentlich hast du a/a'=sin(α)/sin(α')  so dass es scheint dass δ=α'-α?

nimm das Additionstheorem für sin(α+δ) ersetze cos(α) durch √(1-sin^2(α)) und du hast eine einfache Gleichung für sin(α)

woher kennst du δ oder α' sonst musst du genauer sagen, was du kennst.

Gruß lul

Comments

ersetze cos(α) durch √(1-sin²(α))

Warum das?