Wie ermittle ich nun die Koordinaten der Scheitelpunkte für Pa? fa: y=-x²+2ax-a²+3a+3 (a∈ℝ)

Question

Gegeben sind die Funktionen f_a: y=-x²+2ax-a²+3a+3 (a∈ℝ) und g: Y=3x+5,25; D_fa, D_g = ℝ

 

Gruß

Comments

Was genau ist Pa? Hat die Gerade damit etwas zu tun?

Scheitelpunkte ermittelt man mit quadratischer Ergänzung oder, falls du schon ableiten kannst, mit der Ableitung der Funktionsgleichung.

---

Scheitelpunkte für Pa? Für Pappi? Für Vati? Für Pappa? :D

---

Die Aufgabe heißt:

Ermittle die Koordinaten der Scheitelpunkte der Parabeln P_a.

Answer 1

f_a: y=-x²+2ax-a²+3a+3

y ' = -2x + 2a = 0  ==> 2x = 2a ==> x = a

y=-a²+2a^2-a²+3a+3 = 3a+3

S(a | 3a+3)

Ortslinie der Scheitelpunkte:

y = 3x+3

Bitte sorgfältig nachrechnen und Fehler melden.

Answer 2

hi

hallo

wir bringen f(x) = -x² + 2ax - a² + 3a + 3 in die scheitelpunktform.
-x² + 2ax - a² + 3a + 3 =
-(x² - 2ax + a²) + 3a + 3 =
-(x - a)² + 3a + 3

jetzt haben wir
f(x) = -(x - a)² + 3a + 3 in der scheitelpunktform.

wir können die koordinaten der scheitelpunkte als eine funktion von a
ausdrücken: S(a) = (x, y) = (a, 3a + 3)
man sieht, dass der y-wert eines scheitelpunktes von a abhängt.
also können wir die scheitelpunkte als eine funktion von a schreiben:
S(a) = 3a + 3, oder mit der gewohnten variable x:
S(x) = 3x + 3. das ist eine geradengleichung. sie verläuft durch alle
scheitelpunkte der parabelschar f(x) = -x² + 2ax - a² + 3a + 3.

a wird in einer schritten erhöht:





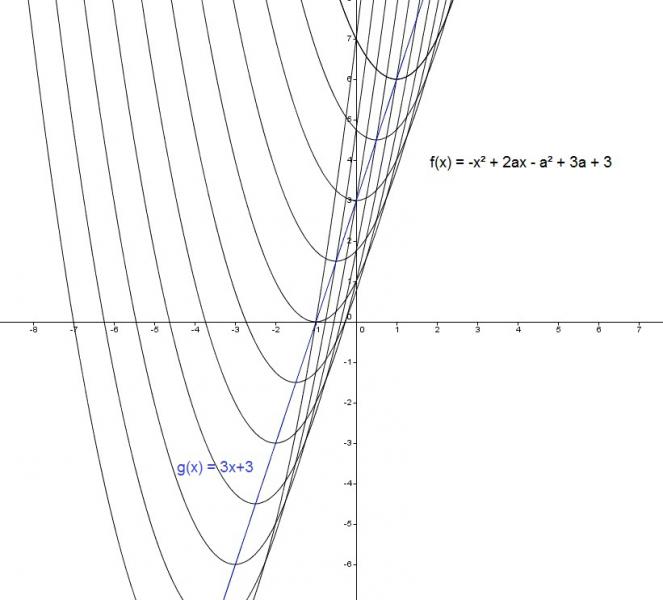
a wird in 0.1 schritten erhöht:

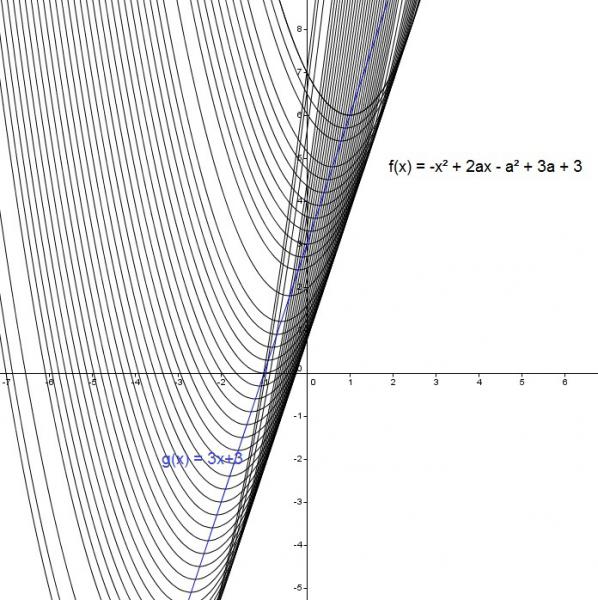
weil a ∈ ℝ ist, gibt es unendlich viele parabeln.