Anteil einer Fläche eines Quadrat

Question

Aufgabe:

Hallo ich habe eine Frage.

Ich versuche es mal zu beschreiben. Gegeben ist ein Quadrat. Die Seitenlänge ist egal. Von einer Seite a wird dann ein Gleichseitiges Dreieck gezeichnet. Dies wird dann auch von der gegenüberliegenden Seite getan also von Seite c. Dadurch entsteht dann in der Mitte eine Raute. Gefragt ist jetzt welchen Anteil die raute von der Quadratfläche einnimmt. Ich hoffe es ist soweit verständlich. .

Answer 1

Hallo Joshi,

Du meinst wahrscheinlich die Raute \(PQRS\)

Die Raute besteht ihrerseits aus zwei gleichseitigen Dreiecken \(\triangle SQR\) und \(\triangle PQS\). Berechne die Höhe \(MR\) eines der Dreiecke und daraus seine Fläche. Die Fläche der Raute ist $$F_{PQRS} = \left( \frac 2{\sqrt 3} - 1\right) \cdot a^2 $$wenn \(a\) die Seite des Quadrats ist.

Falls Du dazu noch Fragen hast, so melde Dich bitte.

Comments

Ich habe jetzt die richtige Lösung. Wie kommen sie aber auf diese Formel?

---

Wie kommen sie aber auf diese Formel?

Es ist die identische Lösung wie bei Mathecoach und mathef (s. dort). Allgemein ist die Höhe \(h\) im gleichseitigen Dreieck mit der Seitenlänge \(s\)$$h = \frac 12  \sqrt 3 \, s \implies s = \frac {2}{\sqrt 3} h$$

Die Höhe \(|RM|\) ist demnach $$|RM| =\left(  \frac 12 \sqrt 3 - \frac 12\right) a = \frac 12 (\sqrt 3 - 1)a$$ und die zugehörige Seitenlänge \(|SQ|\) $$|SQ|= \frac 2{\sqrt 3} |RM| =  \frac 1{\sqrt 3}\left(  \sqrt 3 - 1\right) a$$Die Fläche der Raute ist doppelt so groß wie die Fläche eines der Dreiecke - also$$\begin{aligned} F_{PQRS}&= 2 \cdot \left( \frac 12 |SQ| \cdot |RM|\right) \\ &= |SQ| \cdot |RM| \\ &= \frac 1{\sqrt 3}\left(  \sqrt 3 - 1\right) a \cdot \frac 12 (\sqrt 3 - 1)a\\ &= \frac 1{2 \sqrt 3}\left( \sqrt 3 - 1\right)^2 a^2 \\ &= \frac 1{2 \sqrt 3}(4 - 2\sqrt 3) a^2\\ &= \left( \frac 2{\sqrt 3} - 1\right) a^2\end{aligned}$$

Answer 2

Pythagoras

h^2 + (a/2)^2 = a^2 --> h = √3/2·a

k = √3/2·a - 1/2·a = (√3/2 - 1/2)·a

k = √3/2·b --> b = 2/3·√3·k = 2/3·√3·(√3/2 - 1/2)·a = (1 - √3/3)·a

A = b·k = (1 - √3/3)·a·(√3/2 - 1/2)·a = (2·√3/3 - 1)·a^2 ≈ 0.1547·a^2

Prüfe mal ob das hinkommen kann.

Comments

Das habe ich auch heraus nur anders gerechnet. Danke aber für die schnelle Antwort

Answer 3

Die Höhe des gleichseitigen Dreiecks ist a/2 *√3

Also ist es von der Spitze des gleichseitigen Dreiecks zur

gegenüberliegenden  Seitenmitte des Quadrats

a -  a/2 *√3.

Damit ist die eine Diagonale der Raute

a - 2* (a -  a/2 *√3 ) =  a*(√3 - 1 )

Für die andere Diagonale (bzw. deren Hälfte) kann man

was mit dem Strahlensatz machen:

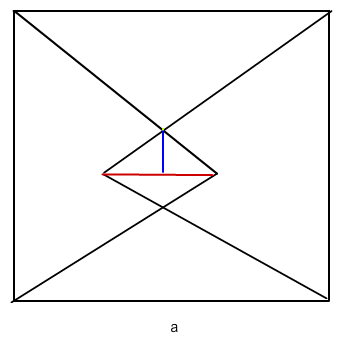
Etwa so: halbe rote Diagonale : halbe andere Diag. (Das blaue)

= Dreieckshöhe  :   (a/2)             Alle Formeln einsetzen gibt  :

 (1-√3)*a/2  :   x    =   a/2 *√3   :  a/2

<=>   (1-√3)*a/2  :   x    =  √3

<=>   (1-√3)*a/2     =  x*√3

<=>   (1-√3)*a    =  x*2√3

<=>   a*(1-√3)/(2√3)     =  x

<=>   a*(3-√3)/6     =  x

Damit ist die Rautenfläche :

(eine Diagonale mal Hälfte der anderen )

A =  a*(√3 - 1 ) * a*(3-√3)/6  = a^2 * (6√3 - 3 )/3 ≈ a^2 * 0,155

Also sind es etwa 15,5% vom Quadrat.

Comments

Ich habe es so gemacht, erst einmal alles berechnet. Dann habe ich die eine Diagonale der Raute berechnet und dann über pythagoras oder trigonometrie die andere Diagonale berechnet. Dann den Flächeninhalt der raute und das geteilt durch das ganze.

Danke trotzdem nochmal

Answer 4

Hallo

die Fläche ist das Produkt der Diagonalen. die kurze kannst du ausrechnen, weil du die Höhe im gleichseitigen Dreieck kennst, die Lange, weil du die Höhe in dem 30° gleichschenkligen Dreieck kennst .

oder du siehst, dass die Raute ähnlich der aus den 2 gleichseitigen Dreiecken ist,

3. Weg, die Fläche der 2 großen Dreiecke+ die 2 restlichen (30°) Dreiecke davon a^2 abziehen ergibt auch deine gesuchte Raute.

Gruß lul