Amplitude und die Periodendauer der Funktion entnehmen

Question

ich benötige Hilfe bei folgender Aufgabe:

Die Abb. A.1 zeigt zwei Funktionen f : t → f(t) und g : t → g(t) mit t $ 0, die jeweils einen Schwingungsvorgang darstellen. Dabei wird der Zeit t (in Sekunden) die Auslenkung s (in Zentimetern) zugeordnet. Der Graph der Funktion f  ist durch Dehnungen aus dem Graph der Sinusfunktion entstanden.

 

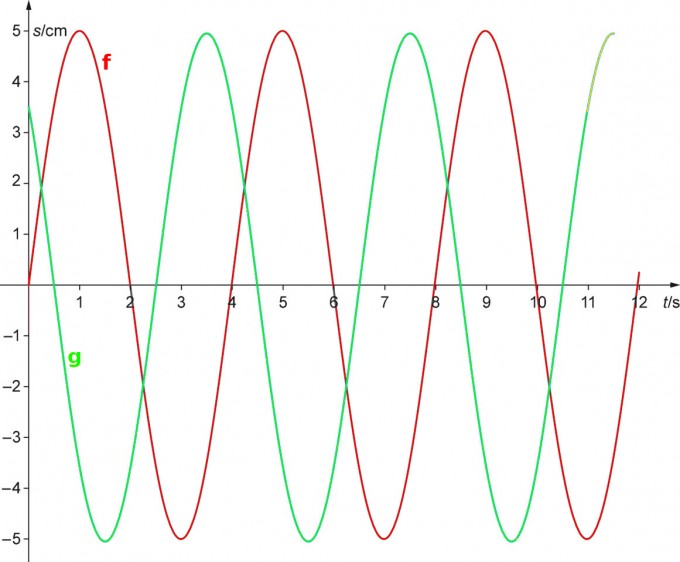
a) Entnehmen Sie der Zeichnung die Amplitude a und die Periodendauer T der Funktion f und geben Sie den Funktionsterm f(t) an.

b) Welche Phasenverschiebung u zeigt der Graph der Funktion g im Vergleich zum Graphen von f ?
      Stellen Sie damit den Funktionsterm g(t) auf.

Ich komme mit beiden Aufgaben leider absolut nicht klar und würde mich über eine Erklärung sehr freuen!

Answer 1

a)

Für beide Funktionen gilt:

Amplitude: 5 cm

Periodenlänge: 4 s

f(t) = 5·SIN(2·pi/4·t)

b)

g(t) = 5·SIN(2·pi/4·(t + 1.5))

Comments

Vielen Dank!

Wie würde dann der Funktionsterm aussehen?

---

Wie würde dann der Funktionsterm aussehen?

Der steht doch in meiner Antwort.

---

Bezieht sich dann g(t) = 5·SIN(2·pi/4·(t + 1.5)) auch auf den Funktionsterm f(t) aus Aufgabe a ?

---

Ich habe f(t) oben noch angefügt. Du hättest doch nur die Verschiebung in x-Achsenrichtung rausnehmen müssen.

Answer 2

Entnehmen Sie der Zeichnung die Amplitude a und die Periodendauer T der Funktion f und geben Sie den Funktionsterm f(t) an.

Amplitude:   größte bzw. kleinste Werte. Beim "normalen" sin sind das 1 und -1 hier 5 und -5, also Amplitude 5

Periode ist normaler Weise  2pi hier aber 4.

Also f(x) = 5 * sin ( t*pi/2 )

g(t) =  5 * sin ( pi/2 *(t - 2.5 ))

Comments

Vielen Dank für Ihre Antwort!

Also statt  f(t) = 5·SIN(2·pi/4·t) dann f(x) = 5 * sin ( t*pi/2 ) ?

---

(2·pi/4)·t = (pi/2) * t =  t*pi/2

ist nur gekürzt bzw. umgestellt.