Konvergenz und Divergenz von Folgen

Question

über jeden Hinweis oder Lösungsvorschläge wäre ich sehr sehr dankbar.
Meine Aufgabe lautet:

Untersuchen Sie die Zahlenfolgen (a_n) auf Konvergenz, bestimmte und unbestimmte Divergenz und geben Sie gegebenenfalls den Grenzwert an:

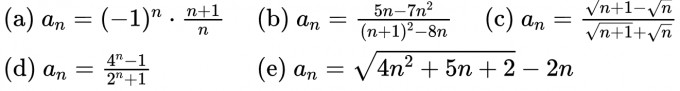
Ich habe mir schon Videos und mein Script angeschaut dazu, aber ich komme einfach nicht weiter/klar.

Zu 4.4. e hätte ich den Grenzwert undzwar 5/4 raus. Aber ich weiß ehrlich gesagt nicht was mir das jetzt genau sagt. Heißt das, dass es konvergent ist? Wenn ja, würde das bedeuten, dass ich für jede Folge hier den Grenzwert bestimmen muss, und wenn es einen gibt, dass die Folge konvergent ist? Wenn nein, dann ist sie divergent?

Über jede Hilfe würde ich mich sehr freuen.

Answer 1

Aloha :)

$$a_n=(-1)^n\frac{n+1}{n}=(-1)^n\left(1+\frac{1}{n}\right)\to(-1)^n$$Die Folge konvergiert nicht, für große \(n\) alterniert sie zwischen \(+1\) und \(-1\).

$$b_n=\frac{5n-7n^2}{(n+1)^2-8n}=\frac{\frac{5}{n}-7}{\left(1+\frac{1}{n}\right)^2-\frac{8}{n}}\to\frac{0-7}{(1+0)^2-0}=-7$$

$$c_n=\frac{\sqrt{n+1}-\sqrt n}{\sqrt{n+1}+\sqrt n}=\frac{\sqrt{n+1}+\sqrt n-2\sqrt n}{\sqrt{n+1}+\sqrt n}=1-\frac{2\sqrt n}{\sqrt{n+1}+\sqrt n}$$$$\phantom{c_n}=1-\frac{2}{\sqrt{1+\frac{1}{n}}+1}\to1-\frac{2}{\sqrt{1+0}+1}=0$$

$$d_n=\frac{4^n-1}{2^n+1}=\frac{2^{2n}-1}{2^n+1}=\frac{(2^n+1)(2^n-1)}{2^n+1}=2^n-1\to+\infty$$Die Folge divergiert gegen Unendlich.

$$e_n=\sqrt{4n^2+5n+2}-2n=\frac{\left(\sqrt{4n^2+5n+2}-2n\right)\left(\sqrt{4n^2+5n+2}+2n\right)}{\sqrt{4n^2+5n+2}+2n}$$$$\phantom{e_n}=\frac{4n^2+5n+2-4n^2}{\sqrt{4n^2+5n+2}+2n}=\frac{5n+2}{2n\left(\sqrt{1+\frac{5}{4n}+\frac{2}{4n^2}}+1\right)}$$$$\phantom{e_n}=\frac{5n}{2n\left(\sqrt{1+\frac{5}{4n}+\frac{2}{4n^2}}+1\right)}+\frac{2}{2n\left(\sqrt{1+\frac{5}{4n}+\frac{2}{4n^2}}+1\right)}$$$$\phantom{e_n}=\frac{5}{2\left(\sqrt{1+\frac{5}{4n}+\frac{2}{4n^2}}+1\right)}+\frac{1}{n\left(\sqrt{1+\frac{5}{4n}+\frac{2}{4n^2}}+1\right)}$$$$\phantom{e_n}\to\frac{5}{2\left(\sqrt{1+0+0}+1\right)}+0=\frac{5}{4}$$

Comments

Vielen vielen Dank :)

Answer 2

a) divergiert (zeigs über Definition mit Fallunterscheidung) [lim sup und lim inf exisitiert]

b) n^2 ausklammern

c) Soll das so heißen?

d) Sandwichsatz

e) Erzeuge ein Binom

Wenn ein Grenzwert exisitiert, so konvergiert die Folge.

Comments

Teile bei d) lieber Zähler und  Nenner durch 2^n.

---

Das geht natürlich sogar schneller!