Du kannst an die Aufgabe ran gehen, indem Du Dir überlegst, wie man ein Element der Menge auch interpretieren kann. Ich unterstelle mal, dass für \(n=3\) \((2,1,0) \ne (1,2,0)\) gilt; d.h. die beiden Anordnungen sind unterschiedlich obwohl sie beide aus dem drei Zahlen 0,1, und 2 bestehen.
So etwas gibt es z.B. als Kooridinate im Raum. Wenn man sich $$k_1+k_2+k_3 = 3$$ als eine Ebenengleichung vorstellt, so ist \(M_3\) die Menge aller Punkte in dieser Ebene mit Koordinaten \(k_i \in \mathbb{N}_0\).
Ich habe Dir mal die beiden Ebenen für \(M_2\) und \(M_3\) eingezeichnet und auch alle Punkte mit ganzzahligen positiven Koordinaten - und damit die Elemente der jeweiligen Menge.
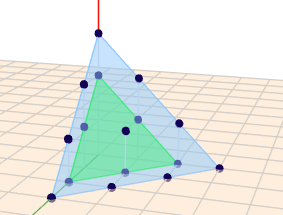
(klick auf das Bild, dann kannst Du die Szene drehen) Fällt Dir was auf?
Die Anzahl der Punkte \(|M_n|\) wächst immer um \(n+1\) gegenüber der vorhergehenden Anzahl. Also $$|M_n| = |M_{n-1}| + n + 1$$und das sind die sogenannten Dreieckszahlen. Für die gilt für das hier benutzte \(n\)
$$|M_n| = \frac 12 (n+1)(n+2)$$Der induktive Beweis, um von der rekursiven Form zur expliziten Form von \(|M_n|\) zu kommen, sollte Dir jetzt nicht so schwer fallen. Falls Du Fragen hast, so melde Dich bitte.