Question

Wie lautet die Ableitung von 1/(3-x) ? und wie kommt man dadrauf?

Ich weiß, dass die Ableitung von 1/x 1/-x² ist, aber wie kann ich den Bruch auseinanderziehen?

danke schonmal

Answer 1

f(x) = 1/3 - x

Die Ableitung wäre nach der Summenregel

f '(x) = 0 - 1 = -1

Aber du meinst sicher

f(x) = 1/(3 - x)

Wichtig ist bitte den Nenner dann vollständig zu klammern. Die Funktion können wir uns umschreiben zu

f(x) = 1/(3 - x) = (3 - x)^-1

Und hier können wir die Kettenregel anwenden die besagt. Äußere Ableitung mal Innere Ableitung:

f '(x) = 1/(3 - x) = -(3 - x)^-2 * -1

Das können wir vereinfachen und wieder Umschreiben

f '(x) = -(3 - x)^-2 * -1 = (3 - x)^-2 = 1/(3 - x)^2

Man könnte es auch mit der Quotientenregel machen. Das ist aber meiner Meinung nach aufwendiger.

Comments

vielen Dank für die Anwort, allerdings sind mir die Kettenregel und die Quotientenregel unbekannt...

---

Dann bleibt dir wohl nur die eigene Herleitung über die h-Methode. Sollt ihr das machen?

---

h-Methode ist mir bekannt, dankeschön :)

Answer 2

Anhand der Graphen von y = 1/x und y=1/(x-3) und y=1/(3-x)

kannst du dir überlegen, wie die Ableitung von y = 1/(3-x) aussehen muss. 

 

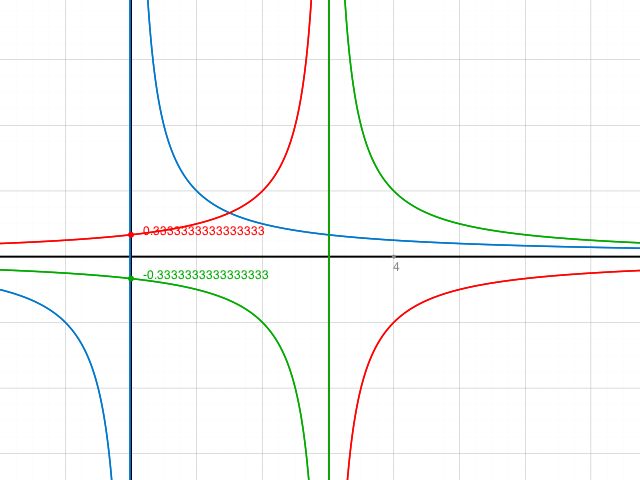
y' = (1/x) ' = -1/ x² und y'= (1/(x-3)) ' = - 1/ ( x-3)² und y' =(1/(3-x))' = 1/(3-x)² =1/ (3-x)²

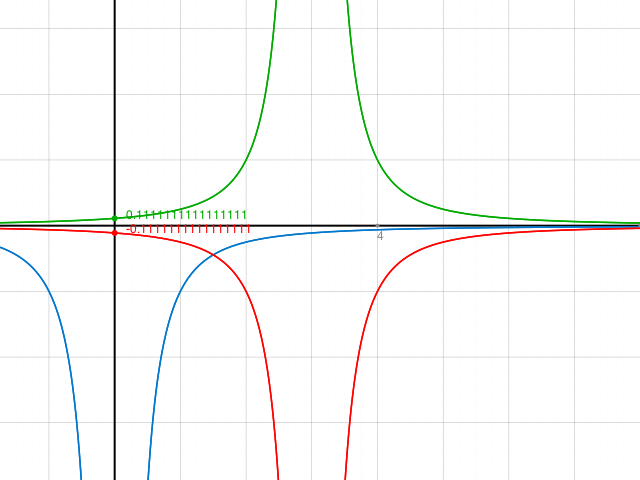
Um das zu berechnen benutzt man normalerweise die Kettenregel.

y = 1/(3-x) hat eine sogenannte inneren Funktion u = 3-x. y ist also 1/ u mit u = 3-x

Du kennst 

(1/u) ' = - 1/u^2

und 

(3-x)' = -1

Die Kettenregel besagt, dass du

y' als Produkt dieser beiden Ableitungen bekommst.

Also y' = (-1/u^2)*(-1) nun vereinfachen und für u=3-x einsetzen

y' = 1/(3-x)^2

Den Beweis der Kettenregel behandelt ihr bestimmt noch in der Schule.

 

 

 

 

Answer 3

Quotientenregel  anwenden, Vorausetzung g≠0

Comments

dankeschön, werden wir demnächst bestimmt auch noch machen :)