Hallo an alle :-)
Ich habe folgende Aufgabe:
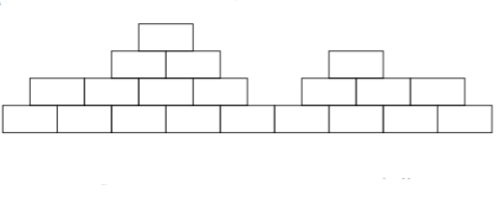
Der Regierungschef eines nicht näher spezifizierten Landes möchte zum Bau einer Mauer an der Landesgrenze unterschiedliche Steine begutachten, nachdem seine Berater ihm mitteilen mussten, dass ein Wassergraben mit Krokodilen leider keine Option ist. Hierzu wurden ihm quaderförmige, gleich große Steine jeder Art mitgebracht und jeweils zu einem Mauerstück aufgebaut. Hierbei soll wie im Diagramm die unterste Reihe aus 9 Steinen bestehen, wobei jeder Stein, außer in der untersten Reihe, mittig auf genau 2 anderen Steinen stehen muss und die unterste Reihe keine Lücken haben
darf. Wir gehen davon aus, dass von jedem Steintypen genügend Steine für jedes der beschriebenen Mauerstücke vorhanden sind. Wie viele Möglichkeiten gibt es, für einen gegebenen Steintypen die Steine zu einem solchen Mauerstück zusammenzusetzen?
Ansatz / Problem :
Ich weiß nicht wie ich das hier angehen soll, aber dennoch habe ich mir etwas überlegt.
Wir wissen, dass es quaderförmige Steine gibt, die gleich groß sind, aber unterschiedliche Arten sind.
Die unterste Reihe der Mauer besteht aus 9 Steinen ohne Lücken und jeder stein der drauf kommt muss mittig auf 2 Steinen der untersten Reihe stehen. Jedoch sind dort die Lücken nicht wichtig (wie auf dem Bild).
Wenn ich es richtig verstanden habe, kann man es mit dem Urnenproblem möglicherweise lösen, also In dem falle Bälle (=Steine) nicht unterscheidbar, da gleich groß, aber die Urne (= jede Reihe der Mauer) unterscheidbar. Und dann Injektiv oder Surjektiv (Unsicher) Verteilt, weil jede 2 Steine einen weiteren Stein haben muss oder weil jede Reihe mind. haben muss.
Also wenn Injektiv dann Berechnung: (m+n-1 über n) und wenn Surjektiv dann: (n-1 über m-1)
Frage:
Hab ich das richtig verstanden ?
für jede Hilfe :-)
EDIT: Nachtrag aus Kommentar:
Also ich habe soeben in einer Mail gesehen, dass gemeint ist, dass wir die Anzahl der Möglichkeiten für einen Mauertsück mit fester Anzahl von Steinen geben sollen und das wir anscheinend auf ein früheres Problem zurück greifen können ... Was mir aber dabei nichts einfällt.
Falls jemand noch eine Idee hat, dann bitte diese stellen :))
Und an allen bedanke ich mich sehr für die Antworten :-)