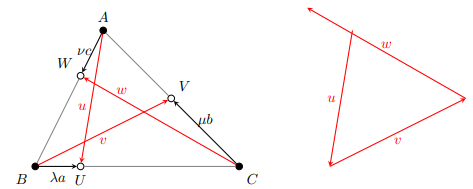
Es seien A, B, C die drei Ecken eines eigentlichen Dreiecks in der Ebene ℝ2
(d.h., die drei Punkte liegen nicht auf einer Geraden). Wir nennen a den Verbindungsvektor von B nach C, in Zeichen: a=\(\vec{BC}\); entsprechend setzen wir b =\(\vec{CA}\) und c =\(\vec{AB}\). Auf jeder der drei Seiten des Dreiecks werde ein weiterer Punkt U, V bzw. W angenommen (siehe nachfolgende Skizze), mit Verbindungsvektoren u =\(\vec{AU}\), v =\(\vec{BV}\) und w =\(\vec{CW}\) zur jeweils gegenüber liegenden Ecke. Es gibt somit drei eindeutig bestimmte reelle Zahlen λ, µ, ν mit 0 ≤ λ, µ, ν ≤ 1, sodass \(\vec{BU}\) = λa, \(\vec{CV}\) = µb und \(\vec{AW}\) = νc.
Welche Bedingung müssen λ, µ, ν erfüllen, damit u, v, w die im Sinne eines Umlaufs orientierten Seitenvektoren eines neuen Dreiecks sind?
Ich bin mir irgendwie total unschlüssig, wie ich an die Sache heran gehen soll.
Wäre cool, wenn mir jemand helfen könnte :)