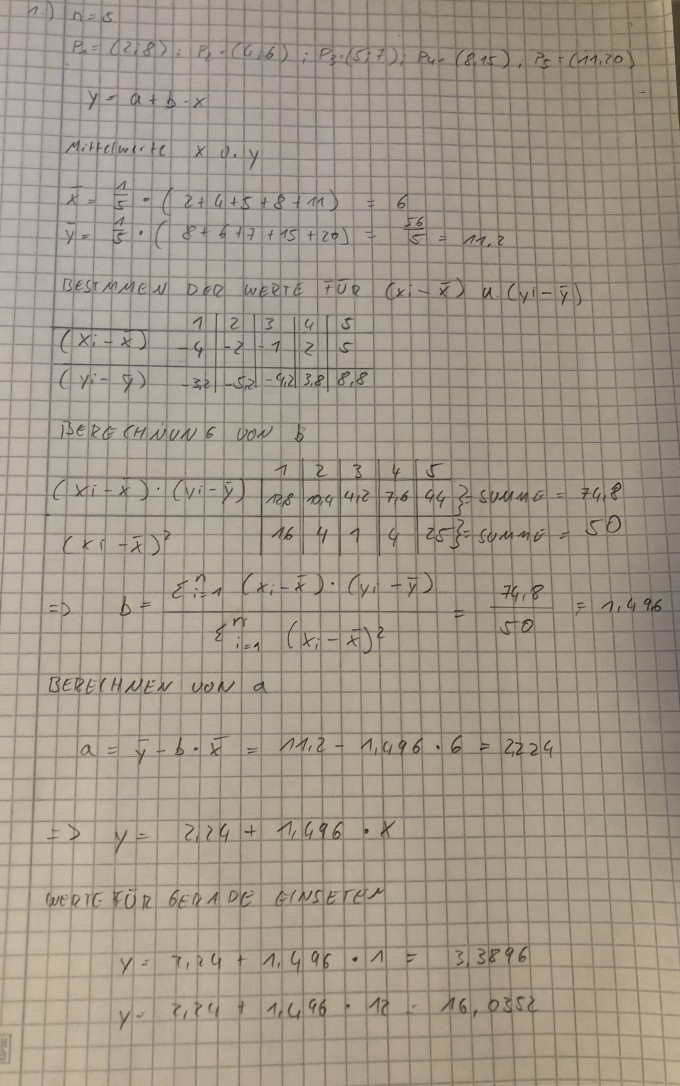Aufgabe:
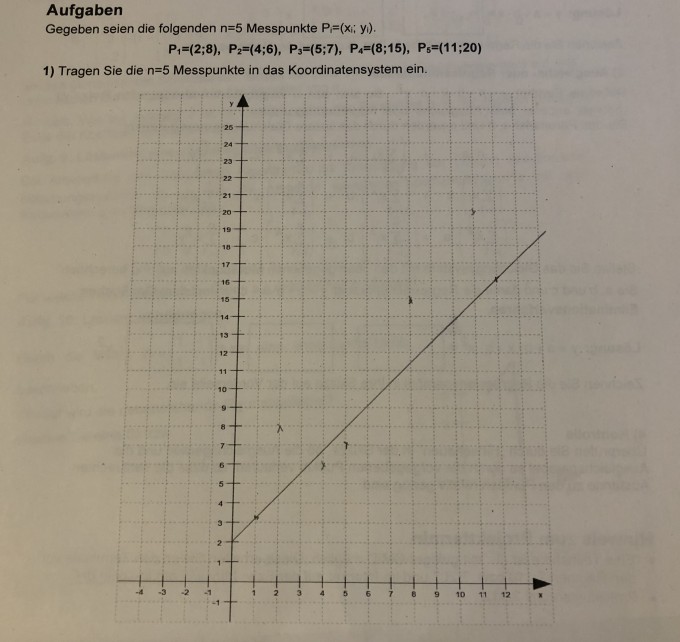
Gegeben seien die folgenden \( n=5 \) Messpunkte \( P_{i}=\left(x_{i} ; y_{i}\right) . \)
\( P_{1}=(2 ; 8), \quad P_{2}=(4 ; 6), \quad P_{3}=(5 ; 7), \quad P_{4}=(8 ; 15), \quad P_{5}=(11 ; 20) \)
1) Tragen Sie die \( n=5 \) Messpunkte in das Koordinatensystem ein.
2) Ausgleichs- oder Regressionsgerade
Diejenige Gerade \( y=a+b \cdot x, \) die sich den \( n \) vorgegebenen Messpunkten \( P_{i}=\left(x_{i} ; y_{i}\right) \), optimal" anpasst (die Summe der Abweichungsquadrate ist minimal), heißt Ausgleichs- oder Regressionsgerade. Die beiden Parameter a und b werden durch das lineare Gleichungssystem bestimmt:
\( \begin{aligned} n \cdot a &+\left(\sum \limits_{i=1}^{n} x_{i}\right) \cdot b=\sum \limits_{i=1}^{n} y_{i} \\\left(\sum \limits_{i=1}^{n} x_{i}\right) \cdot a+\left(\sum \limits_{i=1}^{n} x_{i}^{2}\right) \cdot b &=\sum \limits_{i=1}^{n} x_{i} y_{i} \end{aligned} \)
Stellen Sie das Gleichungssystem mit den oben gegebenen Messpunkten auf und berechnen Sie a und \( b \) und damit die Regressionsgerade \( y=a+b \cdot x \) mit dem Gaußschen Eliminationsverfahren.
Lösung: y = a+b·x = __ + __ ·x
Problem/Ansatz:
Habe ich die Aufgabe so richtig gedeutet :