Ausgleichs- oder Regressionsgerade Schwer

Question

Text erkannt:

Aufgaben Gegeben seien die folgenden \( n=5 \) Messpunkte \( P_{i}=\left(x_{i} ; y_{i}\right) . \)
\( P_{1}=(2 ; 8) \)
\( P_{5}=(11 ; 20) \)
1) Tragen Sie die \( n=5 \) Messpunkte in das Koordinatensystem ein.

Text erkannt:

2) Ausgleichs- oder Regressionsgerade
Diejenige Gerade \( y=a+b \cdot x, \) die sich den \( n \) vorgegebenen Messpunkten \( P_{i}=\left(x_{i} ; y_{i}\right), \) optimal" anpasst (die Summe der Abweichungsquadrate ist minimal), heißt Ausgleichs- oder Regressionsgerade. Die beiden Parameter a und b werden durch das lineare Gleichungssystem bestimmt:
$$ \begin{array}{c} n \cdot a+\left(\sum \limits_{i=1}^{n} x_{i}\right) \cdot b=\sum \limits_{i=1}^{n} y_{i} \\ \left(\sum \limits_{i=1}^{n} x_{i}\right) \cdot a+\left(\sum \limits_{i=1}^{n} x_{i}^{2}\right) \cdot b=\sum \limits_{i=1}^{n} x_{i} y_{i} \end{array} $$
Stellen Sie das Gleichungssystem mit den oben gegebenen Messpunkten auf und berechnen Sie a und \( b \) und damit die Regressionsgerade \( y=a+b \cdot x \) mit dem Gaußschen Eliminationsverfahren.
Lösung: \( y=a+b \cdot x=-+-x \)

Aufgabe:

Problem/Ansatz: Ich hab mir da paar Notizen gemacht bekomme mittelwert raus aber anschießend weiß ich nicht wie ich angehen soll. Könnte einer so freundlich sein und es etwas ausführlicher es erklären wäre sehr dankbar

mfg

Answer 1

Aloha :)

Ich komme auf folgende Summen:$$n=5\quad;\quad\sum\limits_{i=1}^nx_i=30\quad;\quad\sum\limits_{i=1}^ny_i=56\quad;\quad\sum\limits_{i=1}^nx_i^2=230\quad;\quad\sum\limits_{i=1}^nx_iy_i=415$$

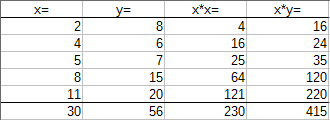
Das führt zu dem Gleichungssystem:

$$\begin{array}{rrrcl}a & b & = && \text{Aktion}\\\hline 5 & 30 & 56 &&:\,5\\30 & 230 & 415 && -6\cdot\text{Zeile 1}\\\hline 1 & 6 & 11,2 && \\0 & 50 & 79 && :\,50\\\hline 1 & 6 & 11,2 && -6\cdot\text{Zeile 2}\\0 & 1 & 1,58 && \\\hline 1 & 0 & 1,72 && \\0 & 1 & 1,58 && \\\hline\end{array}$$

Wir haben also \(a=1,72\) und \(b=1,58\) gefunden. Die Regressionsgerade ist daher:

$$y=1,72+1,58\cdot x$$

~plot~ 1,72+1,58*x ; {2|8} ; {4|6} ; {5| 7} ; {8|15} ; {11|20} ; [[0|12|0|21]] ~plot~

Comments

Ich danke dir..! Hast mir echt gut geholfen