Ich würde gern wissen, wie die Konstruktion auf dem Foto zustande kommt.
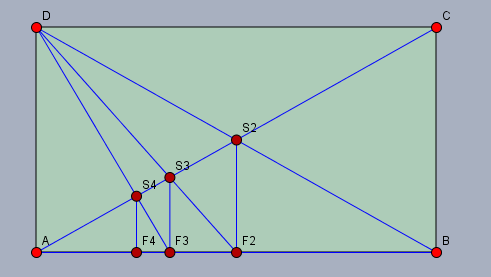
Zeichen ein Rechteck \(ABCD\) und die Diagonalen \(DB\) und \(AC\). Die Diagonalen schneiden sich in \(S_2\). Fälle das Lot von \(S_2\) auf \(AB\); der Fußpunkt ist \(F_2\). Die Gerade durch \(D\) und \(F_2\) schneidet \(AC\) in \(S_3\). Fälle von dort wieder das Lot auf \(AB\) und der Fußpunkt ist \(F_3\) usw.
Mir ist aber unklar, wie die einzelnen Stammbrüche entstehen können ...
Beginne bei einem beliebigen Fußpunkt \(F_i\). Das Verhältnis der Strecken \(|AF_i| \div |AB|\) sei \(\tau\). Ersetze noch \(AB=a\) und \(BC=b\) und stelle die Vektorgleichung für das Dreieck \(\triangle AS_{i+1}D\) auf. Wobei \(x = |AF_{i+1}| \div |AB| = |AS_{i+1}|\div |AC|\) und \(y = |DS_{i+1}| \div |DF_i|\) ist. Und \(x\) ist auch das neue Verhältnis! Die Vektorgleichung lautet: $$\begin{aligned} \vec{DS_{i+1}} - \vec{AS_{i+1}} + \vec{AD} &= 0 \\ \tau y (-b + \tau a) - x (a+b) + b &= 0 \\ -\tau y b + \tau^2 ya - x a - x b + b &= 0 \\ a(\tau^2 y - x) + b(1-\tau y - x) &= 0\end{aligned}$$Die Gleichung geht nur auf, wenn die Koeffizienten vor \(a\) und \(b\) gleich 0 sind. Damit erhält man das Gleichungssystem $$\begin{pmatrix}-1& \tau^2 \\ 1& \tau \end{pmatrix} \cdot \begin{pmatrix} x\\ y\end{pmatrix} = \begin{pmatrix} 0\\ 1\end{pmatrix}$$ Die Lösung für \(x\) ist dann$$x = \frac {\tau^2}{\tau + \tau^2}$$Sei \(\tau = 1/i\) dann wird daraus$$x = \frac{1}{i+1}$$ alles klar?
Gruß Werner