Bestimmen Sie die Gleichung der Tangente von f, die durch den Punkt P(0/1) geht.

Question

f(x) = x - 1/x

Bestimmen Sie die Gleichung der Tangente von f, die durch den Punkt P(0/1) geht.
Kontrollergebnis: t(x) = 5/4 x - 1

Ich komme aber auf: t(x) = 5/4x + 1

Answer 1

f(x) = x - 1/x
f'(x) = 1/x^2 + 1

(f(x) - 1) / (x - 0) = f'(x) --> x = -2

t(x) = f'(-2)·(x + 2) + f(-2) = 1.25·x + 1

Du hast richtig gerechnet und die Kontroll-Lösung ist Müll.

Die Kontroll-Lösung geht durch den Punkt (0 | -1) und nicht durch den Punkt (0 | 1).

~plot~ x-1/x;1.25·x + 1;1.25·x - 1 ~plot~

Comments

!!

Welchen Schnittwinkel hat diese Tangente mit der y-Achse?

--> α ≈ 38.66° ?

---

90° - ARCTAN(1.25) = 38.66°

Jepp. Ist richtig.

---

Hallo, bin in meinem Mathebuch auch an der Aufgabe hängen geblieben und habe die Rechnung hier soweit verstanden und nachvollziehen können. Was ich jedoch nicht verstehe ist, warum man hier einfach davon ausgehen kann, dass die Tangente genau am Schnittpunkt von Funktion und Ableitungsfunktion liegt. Könnte das nochmal erklärt werden?

---

Was ich jedoch nicht verstehe ist, warum man hier einfach davon ausgehen kann, dass die Tangente genau am Schnittpunkt von Funktion und Ableitungsfunktion liegt.

Tut mir leid ich verstehe nicht was du meinst.

---

Mein Fehler, ich hab das etwas missverstanden. Hatte das so verstanden, dass man irgendwie den x-Wert des Schnittpunktes von f und f´ sucht (wegen dem Gleichsetzen), und war verwirrt, woher man weiß, dass die beiden einen Schnittpunkt genau an der Stelle der Tangente haben. Aber es ging ja darum, die identische Steigung zu finden.

Answer 2

Deine Lösung ist richtig, das Kontrollergebnis nicht.

Answer 3

gegeben
f ( x ) = x - 1 / x
P ( 0 | -1 )

Eine Skizze kann hilfreich sein
a.) gegeben
Alle Skizzen sind symbolisch.

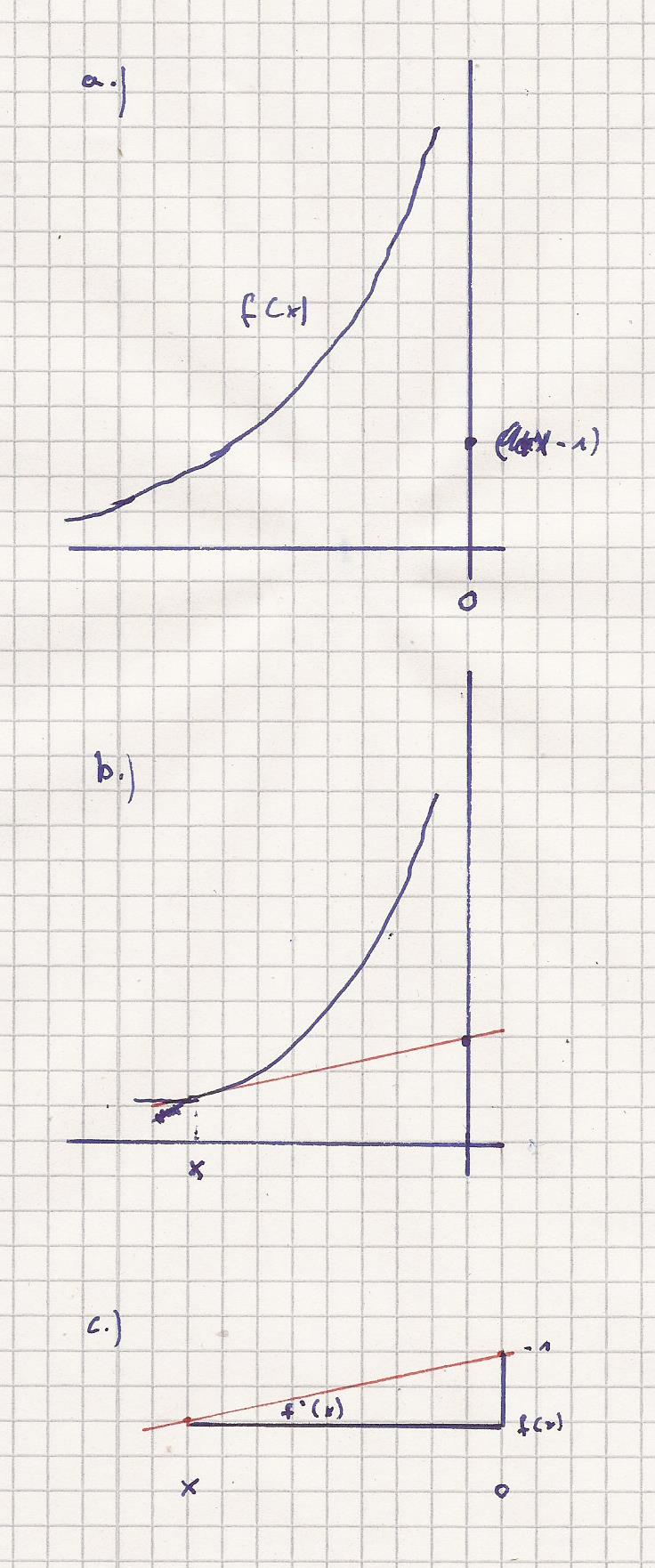
b.) mit der Tangente . x ist der Schnittpunkt
Funktion / Tangente

c.) f ´ ( x ) = 1 + 1/ x^2
Steigung an der Stelle x = Tangentensteigung

Das Steigungsdreick ist

f´( x ) = Δ y / Δ x
f ´( x ) = ( -1 - f ( x ) ) / ( 0 - x )

1 + 1/x^2 = [ -1 - ( x - 1/x ) ]  / [ 0 - x ]
x = 2

f ´( 2 ) = 1 + 1/2 ^2 = 5/4 = m Tangente
t ( x ) = m * x + b
t ( x ) = 5/4 * 2  - 1

Der Graph

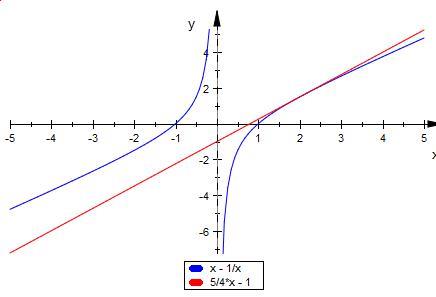
Ob jetzt P ( 0 | -1 ) oder
P ( 0 | 1 ) sein soll weiß weiß ich nicht.
Dann die Rechnung mit dem anderen Wert
durchführen