Amplitudendichtespektrum eines Signals bestimmen. (Fourier Transformation)

Question

Aufgabe:

Das Signal x(t)=exp(−5t)*σ(t) wird auf ein System gegeben, welches durch die Übertragungsfunktion H(w)=1/(5+jw) beschrieben ist.

σ(t) = Einheitssprungfunktion

a) Berechnen Sie das Amplitudendichtespektrum des Eingangssignals mit Hilfe der Fourier-Transformation.

b) Bestimmen Sie das Amplitudendichtespektrum des Ausgangssignals.

Problem/Ansatz:

a) habe ich gemacht. Es kommt raus: X(w) = 1 / (5+jw)

Wie bestimmt man daraus das Amplitudenspektrum??

Answer 1

Angenommen das Eingangssignal ist \( x(t) = e^{-5t} \sigma(t) \), dann gilt

$$ X(\omega) = \frac{1}{5 + j\omega} $$ und deshalb $$  | X(\omega) | = \frac{1}{ \sqrt{25 + \omega^2} } $$

Das Ausgangssignal \( Y(\omega) \) berechnet sich wie folgt

$$ Y(\omega) = H(\omega) X(\omega) = \frac{1}{ (5 + j\omega)^2 } $$ und deshalb

$$ | Y(\omega) | = \frac{1}{ 25 + \omega^2 } $$

Comments

Ok, vielen dank. Ich verstehe das soweit.

Ich habe noch 2 Fragen dazu.

1) Ich habe irgendwie gedacht ich müsste für aufg b.) etwas zeichnen, aber nach deiner Auslegung ist b zumindest rechnerisch, der Betrag der Multiplikation von H(w) und Y(w).

Ich kenne diesen Zusammenhang nur aus Laplace.. H(s) = Y(s)/X(s)

Also gilt dieser Zusammenhang auch für Fourier-Transf.?

2) Ich habe hier eine ähnlich Aufgabe vorliegen.

a) Das dargestellte kontinuierliche Sinussignal wird für 4 Sekunden betrachtet. Für diesen Ausschnitt soll das Amplitudendichtespektrum ermittelt werden. Führen Sie hierzu die Fourier-Transformation durch.

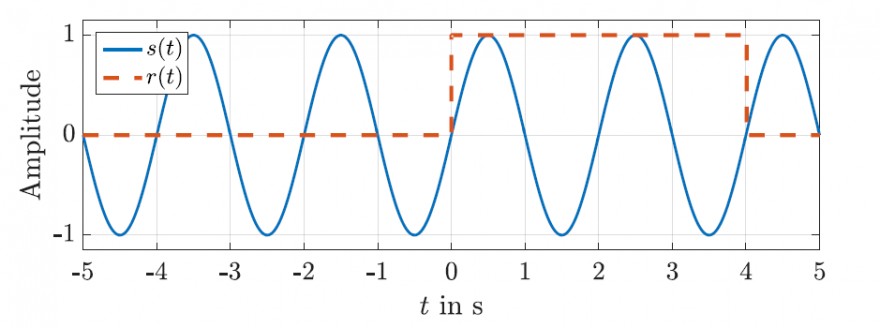
x(t) = s(t) r(t)

b) Geben Sie die Gleichung an, mit der das Amplitudendichtespektrum X(w) aus S(w) und R(w) bestimmt werden könnte, wenn S(w) und R(w) bekannt wären. Keine Rechnung notwendig!

Aufg a) ist hier klar. Für aufg b), ist da der Zusammenhang zw. Fourier und Faltung gemeint?

Dann wäre die Antwort für b)

X(w) = S(w) * R(w)  ??

Wobei * hier der Faltungsoperator ist.

Tausend Dank!!!!!!!!

---

wie berechnest du den Betrag von x(w), von Hand?

---

Versteh Deie Frage nicht. Und bei welcher Aufgabe bist Du. Bei der ursprünglichen oder bei der zweiten?

Übrigens, mach doch bitte bzgl. der zweiten Aufgabe eine neue Frage auf. Sonst kommt man ganz durcheinander.