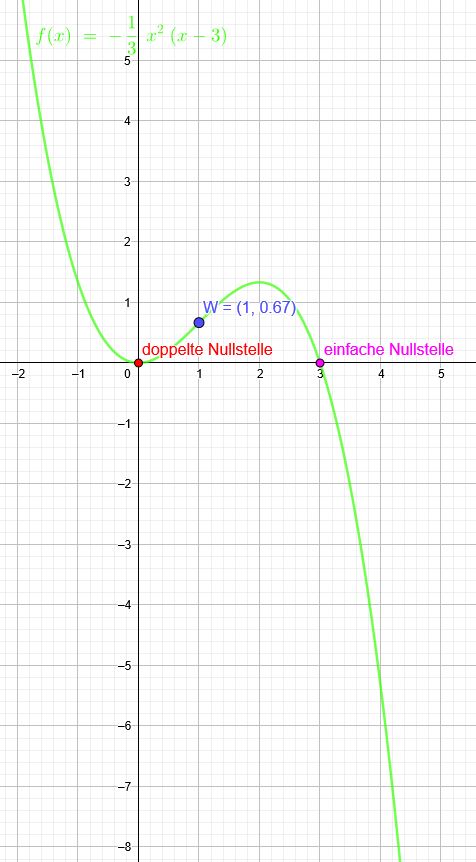
\(y= ax^3 + bx^2 + cx + d\) hat in \(O (0|0)\) einen Extrempunkt und in \(W (1|\frac{2}{3})\) den Wendepunkt. Ermittle die Funktionsgleichung von f.
Lösung über die Nullstellenform der kubischen Parabel
Ein Extrempunkt bei \(O (0|0)\) bedeutet, dass dort ist eine doppelte Nullstelle ist .
\(f(x)=a \cdot x^2(x-N)\)
\(W (1|\frac{2}{3})\)
\(f(1)=a(1-N)\)
\(a \cdot (1-N)=\frac{2}{3}\) → \(a =\frac{2}{3-3N}\)
\(f(x)=\frac{2}{3-3N} \cdot (x^3-x^2 \cdot N)\)
Wendepunkteigenschaft: \(f''(x_W)=0\)
\(f'(x)=\frac{2}{3-3N} \cdot (3x^2-2x\cdot N)\)
\(f''(x)=\frac{2}{3-3N} \cdot (6x-2\cdot N)\)
\(f''(1)=\frac{2}{3-3N} \cdot (6-2\cdot N)\)
\(\frac{2}{3-3N} \cdot (6-2\cdot N)=0\)
\(N=3\) \(a =\frac{2}{3-3 \cdot 3 }=-\frac{1}{3}\)
\(f(x)=-\frac{1}{3} \cdot x^2(x-3)\) Kann noch ausmultipliziert werden.