Zeigen Sie, dass genau dann a×b=0 gilt, wenn a und b linear abhängig sind.

Question

$$ \begin{array}{l} {\text { Seien }} \\ {\qquad a=\left(\begin{array}{l} {a_{1}} \\ {a_{2}} \\ {a_{3}} \end{array}\right), \quad b=\left(\begin{array}{l} {b_{1}} \\ {b_{2}} \\ {b_{3}} \end{array}\right) \in \mathbb{R}^{3}} \end{array} $$
zwei Vektoren im dreidimensionalen Raum. Das Kreuzprodukt \( a \times b \) ist definiert als
$$ a \times b:=\left(\begin{array}{l} {a_{2} b_{3}-a_{3} b_{2}} \\ {a_{3} b_{1}-a_{1} b_{3}} \\ {a_{1} b_{2}-a_{2} b_{1}} \end{array}\right) \in \mathbb{R}^{3} $$

Zeigen Sie, dass genau dann \( a \times b=0 \) gilt, wenn \( a \) und \( b \) linear abhängig sind.

Comments

Hallo, ich weiß nicht warum meine frage verändert wurde?

---

Sieht so aus, als hättest du das selbst geändert.

Text erkannt:

Gepostet vor 3 Tagen von schnuckimucki Zeigen Sie, dass genau dann a \( x b=0 \) gilt, wenn a und b linear abhängig sind. A winfarraytil find.

 

Das hier hattest du ursprünglich gepostet. Dann (gemäss mathelounge-protokoll) geändert wie unten im Kommentar bereits angegeben.

Nun steht oben wieder deine angeblich erste Version der Fragestellung.

---

Wieso sollte ich meine frage umändern???

---

Dann hat halt mathelounge einen Fehler gemacht und den grössten Teil deiner ursprünglichen Frage entfernt. Nun steht oben alles wieder so, wie du es gepostet hattest. Zumindest die erste Version, die in der Fragegeschichte gespeichert ist.

Answer 1

Wann sind die Vektoren [a1, a2] und [b1, b2] linear abhängig. Was müsste dann gelten?

Comments

EDIT: Sieht die Frage so aus, wie das für diese Antwort passt?

Schnuckimucki hat einen grossen Teil der Fragestellung nachträglich entfernt.

Text erkannt:

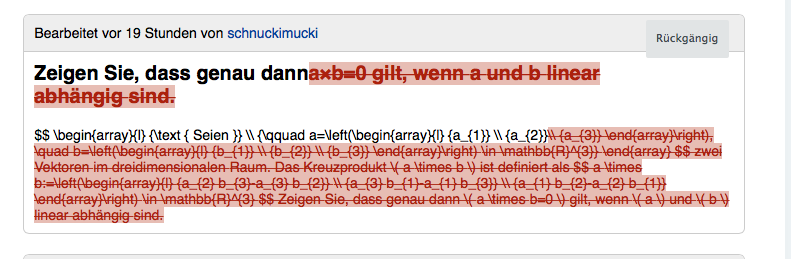
Bearbeitet vor 19 Stunden von schuckimuck
Zeigen Sie, dass genau dannaxbe 0 gilt, wenn a und-b-linear
abhängig-sind.
ss beging th-teart (Sein \( ) \) ) In flaquad a defflobeging fa ( 1) If \( (a,(2) \) ) I end faray wighth
vertuad belefflogoping for Raum Das Kreubrreatimes \( b \) ist afting \( f(x) \) s. Vilms
biellefflobging frafing \( -(3-2)-(3+n) n+6(3+a+1)-(3 n+18-10-12-12-12-10-12-12-12-10-12-12-1000-17) \)
indarablifing sind 888 zeigen Sie. dass ganal dann's bata 19 the wendy fay
linearabling sind:

Habe nun diesen Teil der Bearbeitung rückgängig gemacht.

Weiter zurück komme ich auch in der Bearbeitung nicht.