Aufgabe:
P teilt die Diagonale DB des Quadrats ABCD im Verhältnis 3:1. Der Punkt Q ist der Mittelpunkt der Strecke CD.
Wie groß ist der Winkel QPA?
Problem/Ansatz:
Da die Figur, also das Viereck ein Quadrat ist, sind doch dann die Innenwinkeln, also an den Ecken, alle 90° groß.
Da die Diagonale das Dreieck teilt, befindet sich am Punkt D auf der einen Seite 45° und auf der anderen Seite 45°. Man kann dies wahrscheinlich nach dem Nebenwinkelnsatz nachweisen.
In der Figur finde ich meiner Meinung nach zwei Dreiecke. Das eine Dreieck DQP und das andere Dreieck APB. Meiner Meinung nach sind die beiden Dreiecke nach dem Kongruenzsatz sws kongruent. Da:
1. Beide Dreiecke haben eine 45° Winkel, am Punkt D und am Punkt B. Es sind Nebenwinkeln
2. Am Punkt A ist ein Winkel von 90°. Aber es gibt nach im Dreieck nur 1/4 vom 90°. Durch Stufenwinkeln merkt man diesen Verhältnis am Punkt P und A.
Ich bin mir mit der Erklärung aber nicht sicher.
Bitte die reinbeschrifteten Linien ignorieren oder nutzen. Ich bin mir nicht sicher ob sie halt richtig sind.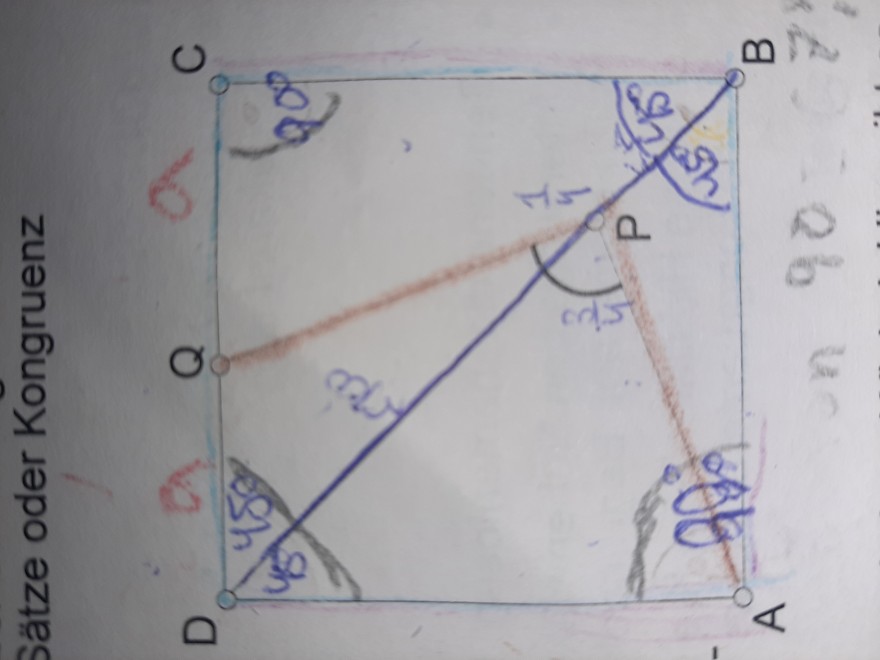
Text erkannt:
\( \% \)
\( 1+23 \)
0
\( \frac{1}{8} \)
\( \frac{8}{8} \)
\( \frac{8}{8} \)