ich schon wieder...
ich verstehe einen Beweis nicht ganz, wäre lieb wenn mir jemand diesen erläutern könnte.
Für K ∈N schreiben wir:
K= KnKn-1.......K1,K0 = Kn*10n+Kn-1*10n-1......K2*102+K1*101 Mit Ki Element aus No mit 0≤Ki≤9 Für alle i(0,1,...,n).
Sei T∈T_10 bel. aber Fest, dann ist 10≡0 mod t
-> 10^i. ich kriege es einfach nicht wieder runter, deshalb hefte ich jetzt einfach mal ein Bild dran.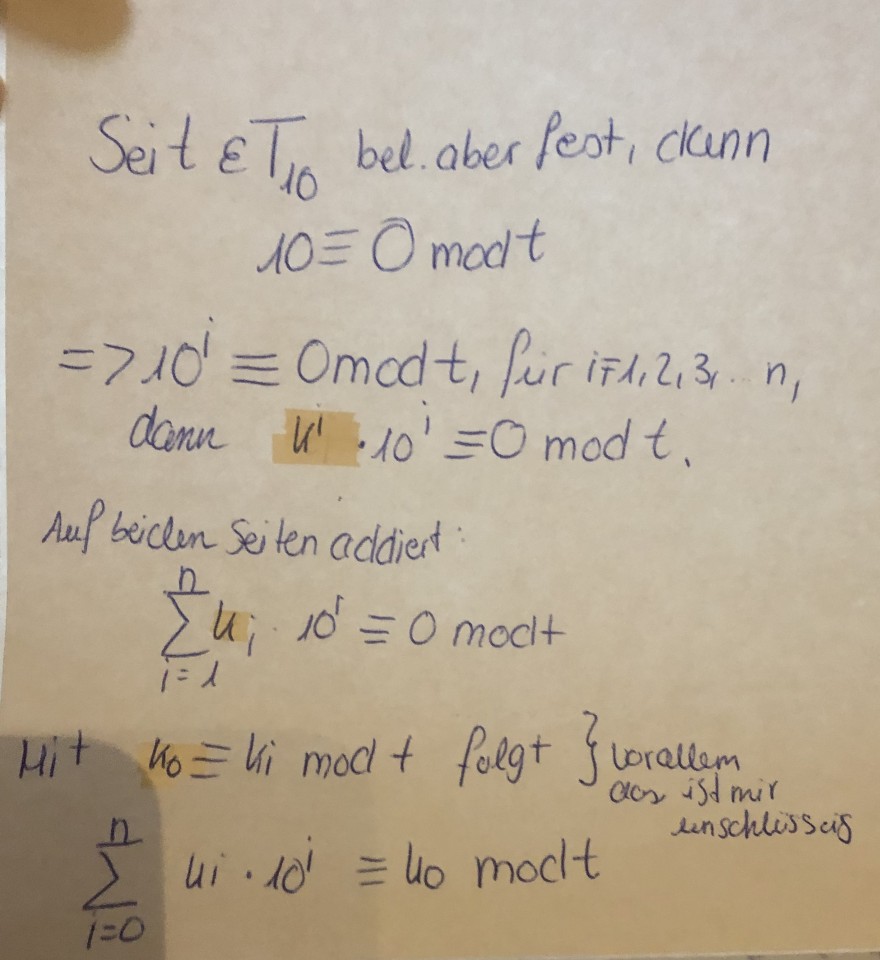
Text erkannt:
Seit \( \varepsilon T_{10} \) bel. aber Peot, denn \( 10 \equiv 0 \) mod \( t \)
\( =>10^{i} \equiv 0 \mathrm{mod} t_{1} \) für \( i=1,2,3, n \)
\( \operatorname{dom} n \quad u^{\prime} \cdot 10^{i}=0 \bmod t \)
Au beiclen Se ten addiert:
\( \sum \limits_{i=1}^{n} u_{i} \cdot 10^{\prime}=0 \) moct
\( M+\quad k_{0}= \) li mod \( + \) folgt \( \int \) urallem \( \sum \limits_{i=0}^{n} u_{i} \cdot 10^{i} \equiv u_{0} \) modt
enschliss cis